2011年初中毕业升学考试(山东济宁卷)数学
在一次数学竞赛中,某小组6名同学的成绩(单位:分)分别是69、75、86、92、95、88.这组数据的中位数是( )
| A.79 | B.86 | C.92 | D.87 |
如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,DE是△ABC的中位线,则DE的长度是( )
| A.3 |
| B.4 |
| C.4.8 |
| D.5 |
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
| A.2 |
| B.4 |
C. |
D. |
掷一枚质地均匀的正方体骰子,骰子的六个面上分别有1至6的点数,则向上一面的点数是偶数的概率__________。
如图:AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠AEF.EG⊥FG于点G,若∠BEM=50°,则∠CFG= __________。
我国以2010年11月1日零时为标准时点进行了第六次全国人口普查,结果公布全国总人口为1370536875人,请将这个数据用科学记数法(保留三个有效数字)表示约为__________。
若用半径为12,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥底面圆的半径的长__________。
如图,在梯形ABCD中,AD∥BC,AB=DC,AC⊥BD于点O,过点A作AE⊥BC于点E,若BC=2AD=8,则tan∠ABE=__________。
菱形OCAB在平面直角坐标系中的位置如图所示,点O的坐标是(0,0),点A在y轴的正半轴上,点P是菱形对角线的交点,点C坐标是(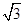 ,3)若把菱形OCAB绕点A逆时针旋转90°,则点P的对应点P′的坐标是__________。
,3)若把菱形OCAB绕点A逆时针旋转90°,则点P的对应点P′的坐标是__________。
为庆祝建党90周年,,某校开展学党史活动,学校决定围绕“你最喜欢的了解党史的途径是什么”的问题,在全校范围内随机抽取部分学生进行问卷调查.问卷要求学生从“自己阅读、听讲座、网上查找资料、其他形式”四种途径任选一种,学校将收集的调查问卷适当整理后,绘制成如图所示的两幅不完整的统计图,请根据统计图所给的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)请补全下面的条形统计图和扇形统计图;
(3)如果全校有1500名学生,请你估计全校最喜欢“网上查找资料”这种途径的学生约有多少名?
如图,现有三张质地和大小完全相同的不透明的纸牌,A、B、C,其正面画有菱形、等边三角形、正六边形,纸牌的背面完全相同,现将这三张纸牌背面朝上洗匀后随机抽出一张,再从剩下的纸牌中随机抽出一张,用画树状图或列表法,求两次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)
某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
如图,⊙O的直径AB与弦CD(不是直径)相交于点E,且CE=DE,过点B作CD得平行线AD延长线于点F.
(1)求证:BF是⊙O的切线;
(2)连接BC,若⊙O的半径为4,sin∠BCD=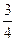 ,求CD的长?
,求CD的长?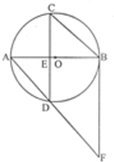
如图,港口B在港口A的西北方向,上午8时,一艘轮船从港口A出发,以15海里∕时的速度向正北方向航行,同时一艘快艇从港口B出发也向正北方向航行,上午10时轮船到达D处,同时快艇到达C处,测得C处在D处得北偏西30°的方向上,且C、D两地相距100海里,求快艇每小时航行多少海里?(结果精确到0.1海里∕时,参考数据 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
我省某工艺厂为全运会设计了一款成本为每件20元得工艺品,投放市场进行试销后发现每天的销售量y(件)是售价x(元∕件)的一次函数,当售价为22元∕件时,每天销售量为780件;当售价为25元∕件时,每天的销售量为750件.
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不能超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)
据统计部门报告,我市去年国民生产总值为238 770 000 000元, 那么这个数据
用科学记数法表示为
| A.2. 3877×10 12元 | B.2. 3877×10 11元 |
| C.2 3877×10 7元 | D.2387. 7×10 8元 |
若一个三角形三个内角度数的比为2︰7︰4,那么这个三角形是
| A.直角三角形 | B.锐角三角形 |
| C.钝角三角形 | D.等边三角形 |
已知⊙O1与⊙O2相切,⊙O1的半径为9 cm,⊙O2的半径为2 cm,则O1O2的长
是
| A.1 cm | B.5 cm | C.1 cm或5 cm | D.0.5cm或2.5cm |
如图,是张老师出门散步时离家的距离 与时间
与时间 之间的函数关系的图象,若用
之间的函数关系的图象,若用
黑点表示张老师家的位置,则张老师散步行走的路线可能是
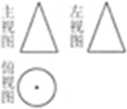
如图,是有几个相同的小正方体搭成的几何体的三种视图, 则搭成这个几何体
的小正方体的个数是
| A.3个 | B.4个 | C.5个 | D.6个 |

如图,如果从半径为9cm的圆形纸片剪去 圆周的一个扇形,将留下的扇形围成
圆周的一个扇形,将留下的扇形围成
一个圆锥(接缝处不重叠),那么这个圆锥的高为
| A.6cm | B. cm cm |
C.8cm | D. cm cm |

在一次夏令营活动中,小霞同学从营地 点出发,要到距离
点出发,要到距离 点
点
 的
的 地
地
去,先沿北偏东 方向到达
方向到达 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了
 到达目的地
到达目的地 ,
,
此时小霞在营地 的
的
A.北偏东 方向上 方向上 |
B.北偏东 方向上 方向上 |
C.北偏东 方向上 方向上 |
D.北偏西 方向上 方向上 |
某校举行以“保护环境,从我做起”为主题的演讲比赛.经预赛,七、八年级各
有一名同学进入决赛,九年级有两名同学进入决赛.前两名都是九年级同学的概率
是 .
如图,是一张宽 的矩形台球桌
的矩形台球桌 ,一球从点
,一球从点 (点
(点 在长边
在长边 上)
上)
出发沿虚线 射向边
射向边 ,然后反弹到边
,然后反弹到边 上的
上的 点. 如果
点. 如果 ,
, .
.
那么 点与
点与 点的距离为 .
点的距离为 .
上海世博会自2010年5月1日到10月31日,历时184天.预测参观人
数达7000万人次.如图是此次盛会在5月中旬入园人数的统计情况.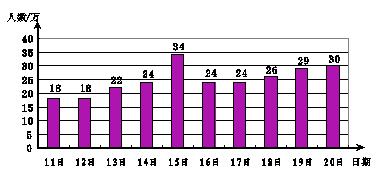
(1)请根据统计图完成下表.
| |
众数 |
中位数 |
极差 |
| 入园人数/万 |
|
|
|
(2)推算世博会期间参观总人数与预测人数相差多少?
观察下面的变形规律: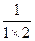 =1-
=1-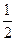 ;
; 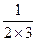 =
=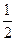 -
-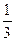 ;
;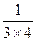 =
=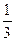 -
-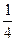 ;……
;……
解答下面的问题:
(1)若n为正整数,请你猜想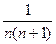 = ;
= ;
(2)证明你猜想的结论;
(3)求和: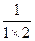 +
+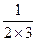 +
+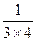 +…+
+…+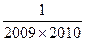 .
.
如图, 为
为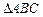 外接圆的直径,
外接圆的直径,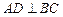 ,垂足为点
,垂足为点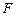 ,
,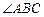 的平分线交
的平分线交 于点
于点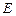 ,连接
,连接 ,
,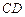 .
.
(1) 求证: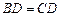 ;
;
(2) 请判断 ,
, ,
, 三点是否在以
三点是否在以 为圆心,以
为圆心,以 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.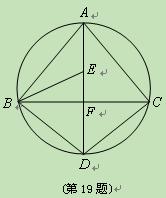
如图,正比例函数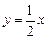 的图象与反比例函数
的图象与反比例函数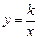
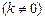 在第一象限
在第一象限
的图象交于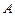 点,过
点,过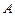 点作
点作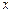 轴的垂线,垂足为
轴的垂线,垂足为 ,已知
,已知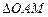 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果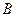 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点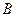 与点
与点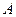 不重合),且
不重合),且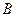 点的横坐标为1,在
点的横坐标为1,在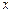 轴上求一点
轴上求一点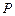 ,使
,使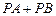 最小.
最小.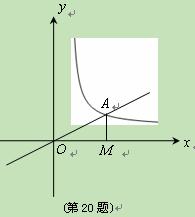
某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
数学课上,李老师出示了这样一道题目:如图 ,正方形
,正方形 的边长为
的边长为 ,
, 为边
为边 延长线上的一点,
延长线上的一点, 为
为 的中点,
的中点, 的垂直平分线交边
的垂直平分线交边 于
于 ,交边
,交边 的延长线于
的延长线于 .当
.当 时,
时, 与
与 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过 作直线平行于
作直线平行于 交
交 ,
, 分别于
分别于 ,
, ,如图
,如图 ,则可得:
,则可得: ,因为
,因为 ,所以
,所以 .可求出
.可求出 和
和 的值,进而可求得
的值,进而可求得 与
与 的比值.
的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
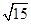 最接近的数是( )
最接近的数是( ) 的根( )
的根( ) ,
,



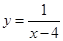 中的自变量x的取值范围__________。
中的自变量x的取值范围__________。
 .
.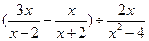 ,其中
,其中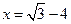 .
.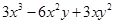 分解因式,结果正确的是
分解因式,结果正确的是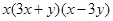
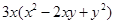
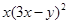
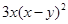
 ,则
,则 的值为
的值为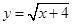 中, 自变量
中, 自变量 的取值范围是 .
的取值范围是 .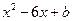 可化为
可化为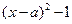 ,则
,则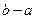 的值是 .
的值是 . 是
是 经过某种变换后得到的图形.如果
经过某种变换后得到的图形.如果
 ,
, ),那么它的对应点
),那么它的对应点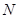 的坐标为 .
的坐标为 .
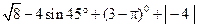
 ,
, )的抛物线交
)的抛物线交 轴于
轴于 点,交
点,交 轴于
轴于 ,
, 两点(点
两点(点 ,
, ).
). 的垂线交抛物线于点
的垂线交抛物线于点 , 如果以点
, 如果以点 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴 与⊙
与⊙ 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 的面积最大?并求出此时
的面积最大?并求出此时
 粤公网安备 44130202000953号
粤公网安备 44130202000953号