2011年初中毕业升学考试(浙江杭州卷)数学
如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.
求证:(1)△ABC∽△POM;(2)2OA2=OP•BC.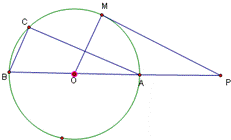
根据给出的下列两种情况,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写做法,但需保留作图痕迹);并根据每种情况分别猜想:∠A与∠B有怎样的数量关系时才能完成以上作图?并举例验证猜想所得结论.
(1)如图①△ABC中,∠C=90°,∠A=24°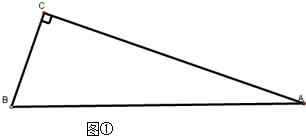
①作图:
②猜想:
③验证:
(2)如图②△ABC中,∠C=84°,∠A=24°.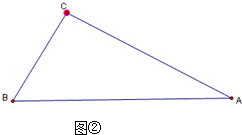
①作图:
②猜想:
③验证:
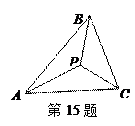
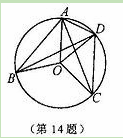
如图,在
中,点
是
边上(端点除外)的一个动点,过点
作直线
.设
交
的平分线于点
 ,交
的外角平分线于点
,连接
、
.那么当点
运动到何处时,四边形
是矩形?并证明你的结论.
,交
的外角平分线于点
,连接
、
.那么当点
运动到何处时,四边形
是矩形?并证明你的结论.

如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米.
(1)请建立适当的直角坐标系,求抛物线的函数解析式;
(2)为了安全美观,现需在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P?(无需证明)
(3)为了施工方便,现需计算出点O、P之间的距离,那么两根支柱用料最省时点O、P之间的距离是多少?(请写出求解过程)
根据2010年第六次全国人口普查主要数据公报,江西省常住人口约为4456万人.这个数据可以用科学计数法表示为( ).
| A.4.456×107人 | B.4.456×106人 | C.4456×104人 | D.4.456×103人 |
下列运算正确的是( ).
| A.a+b=ab | B. a2·a3=a5 | C.a2+2ab-b2=(a-b)2 | D.3a-2a=1 |
把点A(-2,1)向上平移2个单位,再向右平移3个单位后得到B,点B的坐标是( ).
| A.(-5,3) | B.(1,3) | C.(1,-3) | D.(-5,-1) |
已知一次函数y=x+b的图象经过第一、二、三象限,则b的值可以是( ).
| A.-2 | B.-1 | C.0 | D.2 |
已知x=1是方程x2+bx-2=0的一个根,则方程的另一个根是( ).
| A.1 | B.2 | C.-2 | D.-1 |
如图,在下列条件中,不能证明△ABD≌△ACD的是( ).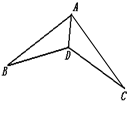
| A.BD=DC,AB=AC | B.∠ADB=∠ADC,BD=DC |
| C.∠B=∠C,∠BAD=∠CAD | D.∠B=∠C,BD=DC |
时钟在正常运行时,分针每分钟转动6°,时针每分钟转动0.5°.在运行过程中,时针与分针的夹角会随着时间的变化而变化.设时针与分针的夹角为y(度),运行时间为t(分),当时间从12︰00开始到12︰30止,y与 t之间的函数图象是( ).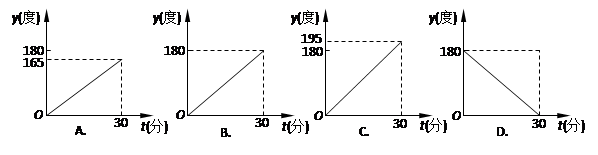
如图所示,两块完全相同的含30°角的直角三角板叠放在一起,∠DAB =30°,有以下四个结论:①AF⊥BC ②△ADG≌△ACF ③O为BC的中点 ④AG︰DE=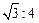 ,其中正确结论的序号是 .
,其中正确结论的序号是 .
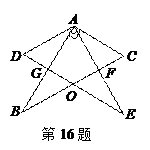 |
.
甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0).
(1)求点D的坐标;
(2)求经过点C的反比例函数解析式.
在平面直角坐标系 中,以点(-3,4)为圆心,4为半径的圆
中,以点(-3,4)为圆心,4为半径的圆
A.与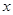 轴相交,与 轴相交,与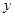 轴相切 轴相切 |
B.与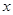 轴相离,与 轴相离,与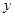 轴相交 轴相交 |
C.与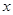 轴相切,与 轴相切,与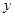 轴相交 轴相交 |
D.与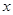 轴相切,与 轴相切,与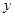 轴相离 轴相离 |
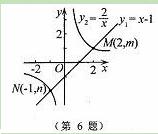
如图,函数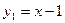 和函数
和函数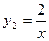 的图像相交于点M(2,
的图像相交于点M(2,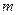 ),N(-1,
),N(-1,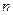 ),
),
若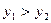 ,则
,则 的取值范围是
的取值范围是
A.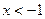 或 或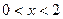 |
B.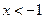 或 或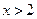 |
C.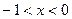 或 或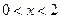 |
D.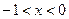 或 或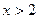 |
在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它
们的面积分别为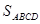 和
和 ,现给出下列命题:
,现给出下列命题:
①若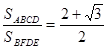 ,则
,则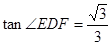 ; ②若
; ②若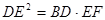 ,则DF=2AD
,则DF=2AD
则
| A.①是真命题,②是真命题 | B.①是真命题,②是假命题 |
| C.①是假命题,②是真命题 | D.①是假命题,②是假命题 |
数据9.30,9.05,9.10,9.40,9.20,9.10的众数是___________;中位数是
_______________
在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线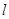 ∥AB,F是
∥AB,F是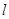 上的一点,且AB=AF,则点F到直线BC的距离为__________
上的一点,且AB=AF,则点F到直线BC的距离为__________
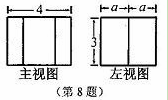
(本小题满分6分)
四条线段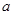 ,
,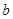 ,
,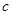 ,
,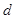 如图,
如图,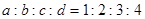
(1)选择其中的三条线段为边作一个三角形(尺规作图,要求保留作图痕迹,不必写出作法);
(2)任取三条线段,求以它们为边能作出三角形的概率
(本小题满分6分)在△ABC中,AB=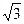 ,AC=
,AC=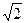 ,BC=1。
,BC=1。
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积。
(本小题满分8分)中国国际动漫节以“动漫的盛会,人民的节日”为宗旨,以
“动漫我的城市,动漫我的生活”为主题,已在杭州成功举办七届。目前,它成为国内规模
最大、交易最旺、影响最广的动漫专业盛会。
下面是自首届以来各届动漫产品成交金额统计图表(部分未完成):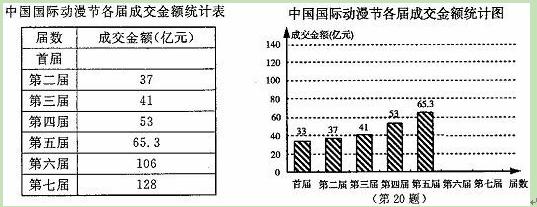
(1)请根据所给的信息将统计图表补充完整;
(2)从哪届开始成交金额超过百亿元?相邻两届中,哪两届的成交金额增长最快?
(3)求第五届到第七届的平均增长率,并用它预测第八届中国国际动漫节的成交金额(精确到亿元)
(本小题满分8分)在平面上,七个边长为1的等边三角形,分别用①至⑦表示
(如图)。从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①
②③组成的图形拼成一个正六边形
(1)你取出的是哪个三角形?写出平移的方向和平移的距离;
(2)将取出的三角形任意放置在拼成的正六边形所在平面,问:正六边形没有被三角形盖住的面积能否等于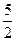 ?请说明理由。
?请说明理由。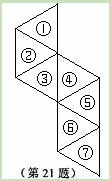
(本小题满分10分)在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,
对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F。
(1)求证:△FOE≌△DOC;
(2)求sin∠OEF的值;
(3)若直线EF与线段AD,BC分别相交于点G,H,求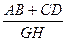 的值。
的值。
(本小题满分10分)设函数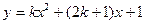 (
( 为实数)
为实数)
(1)写出其中的两个特殊函数,使它们的图像不全是抛物线,并在同一直角坐标系中,用描点法画出这两个特殊函数的图像;
(2)根据所画图像,猜想出:对任意实数 ,函数的图像都具有的特征,并给予证明;
,函数的图像都具有的特征,并给予证明;
(3)对任意负实数 ,当
,当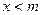 时,
时,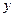 随着
随着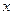 的增大而增大,试求出
的增大而增大,试求出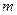 的一个值
的一个值
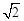
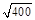

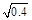
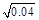

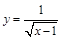
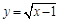
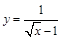
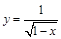
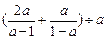 ,其中
,其中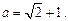
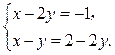

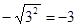
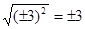
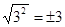
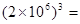
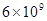
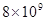
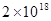
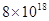
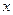 ,
,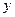 的两部分,则
的两部分,则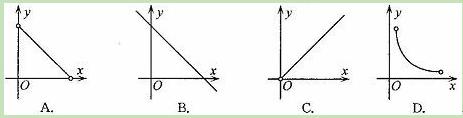
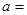
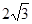
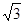
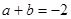 ,且
,且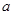 ≥2
≥2 ,则
,则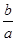 有最小值
有最小值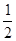
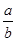 有最大值2
有最大值2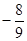
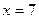 时,代数式
时,代数式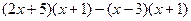 的值为__________
的值为__________
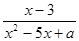 ,当
,当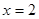 时,分式无意义,则
时,分式无意义,则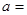 _______;当
_______;当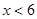 时,
时,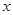 的值共有_______个
的值共有_______个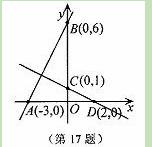
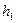 ,
,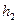 ,△OEF与△OGH组成的图形称为蝶形。
,△OEF与△OGH组成的图形称为蝶形。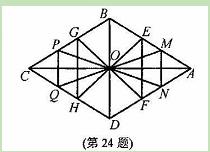
 粤公网安备 44130202000953号
粤公网安备 44130202000953号