2011年初中毕业升学考试（浙江湖州卷）数学

任意写出一对互为倒数的数：________ 和 _______.

某班有女生a人，男生比女生的2倍少5人，则男生有___________________人.

不等式组 的解集是__________.

如图1，在要使,则需增加条件_____________（限写一个）.                                 

如图2，A、B两点位于一个池塘的两端，冬冬想用绳子测量A、B两点间的距离，但绳子不够长，一位同学帮他想了一个办法：先在地上取一个可以直接到达A、B的点C，找到AC，BC的中点D、E，并且测得DE的长为15m，则A、B两点间的距离为__________.
 图2

下列各数：、、、、0.01020304…中是无理数的
有_____________________.

一个圆锥形的蛋筒，底面圆直径为7cm，母线长为14cm，把它的包
装纸展开，侧面展开图的面积为__________________cm²(不计折叠部分).

如图3，四边形ABCD是O的内接四边形，∠DCE＝，则            

∠BAD＝______________.                                                

－4的绝对值是                                              （     ）
A. 4             B.             C. －4             D.  

函数中，自变量x的取值范围是                       (       )
A. x < 1           B. x ≤ 1        C. x > 1             D. x≥1     

下列运算中
(1)          (2)           (3)
(4)      (5)
其中正确的运算有                                                   (      )
A. 1个          B. 2个               C. 3个              D. 4个

A.          B.                  C.                D.

下列图案中不是中心对称图形的是                                     （    ）
 

 

下面式子从左边到右边的变形中是因式分解的是                         （    ）
A.              B.          
C.               D.

方程的左边配成完全平方后所得方程为                   （    ）
A.     B.      C.    D. 以上答案都不对

在一个四边形ABCD中，依次连结各边中点的四边形是菱形，则对角线AC与BD需要满足条件                                                            （    ）
A. 垂直          B. 相等             C.垂直且相等      D. 不再需要条件

下列命题中，正确的命题是                                           （    ）
A. 有两条边和其中一条边所对的角相等的两个三角形是全等三角形
B. 相似三角形面积之比等于相似比
C. 任意多边形的外角和都等于
D. 过切点的直线是圆的切线

一个正常人在做激烈运动时，心跳速度加快，当运动停止下来后，心跳次数N(次)与时间s(分)的函数关系图像大致是  （     ）





                                            
 
 
A                   B                  C                 D

计算：

某中学在一次法律知识测试中，抽取部分学生成绩（分数为整
数，满分100分）将所得得数据整理后，画出频率分布直方图，已
知图中从左到右的三个小组的频率分别为0.04，0.06，0.82，第二
小组的频数为3.
(1)本次测试中抽样的学生有多少人？
(2)分数在90.5～100.5这一组的频率是多少？有多少人？                   
(3)若这次成绩在80分以上（含80分）为优秀，则优秀率不低于多少？
                                                                     

如图7，有两棵树，一棵高10米，另一棵高4米，两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多少米？

		图7

证明题24．如图8，在  ABCD中，DE＝BF.

求证：四边形AFCE是平行四边形.

（11·湖州）－5的相反数是

A．5

B．－5

C．

D．

（11·湖州）计算a²·a³，正确的结果是

（11·湖州）根据全国第六次人口普查统计，湖州市常住人口约为2890000人，近
似数2890000用科学记数法可表示为

（11·湖州）如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的
值为

A． 2

B．

C．

D．

（11·湖州）数据1，2，3，4，5的平均数是

（11·湖州）下列事件中，必然事件是

（11·湖州）下列图形中，经过折叠不能围成一个立方体的是

（11·湖州）如图，已知△AOB是正三角形，OC⊥OB，OC=OB，将△OAB绕点
O按逆时针方向旋转，使得OA与OC重合，得到△OCD，则旋转的角度是

（11·湖州）如图，已知AB是⊙O的直径，C是AB延长线上一点，BC=OB，
CE是⊙O的切线，切点为D，过点A作AE⊥CE，垂足为E，则CD：DE的值是

A．

B．1

C．2

D．3

（11·湖州）如图，已知A、B是反比例函数（k＞0，x＜0）图象上的两
点，BC∥x轴，交y轴于点C。动点P从坐标原点O出发，沿O→A→B→C（图中“→”
所示路线）匀速运动，终点为C。过P作PM⊥x轴，PN⊥y轴，垂足分别为M、N。设四
边形OMPN的面积为S，P点运动时间为t，则S关于t的函数图象大致为

（11·湖州）当x=2时，分式的值是▲。

（11·湖州）如图，已知CD平分∠ACB，DE∥AC，∠1=30°，则∠2=▲度。

（11·湖州）某校对初三（2）班40名学生体育考试中“立定跳远”项目的得分情况进行了统计，结果如下表，

根据表中数据，若随机抽取该班的一名学生，则该学生“立定跳远”得分恰好是10分的概率是▲。

（11·湖州）如图，已知梯形ABCD，AD∥BC，对角线AC，BD相交于点O，
△AOD与△BOC的面积之比为1：9，若AD=1，则BC的长是▲。

（11·湖州）如图，已知抛物线经过点（0，－3），请你确定一个
b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间。你确定的b的值是▲。

（11·湖州）如图，甲类纸片是边长为2的正方形，乙类纸片是边长为1的正方
形，丙类纸片是长、宽边长分别是2和1的长方形。现有甲类纸片1张，乙类纸片4张，则
应至少取丙类纸片▲张才能用它们拼成一个新的正方形。

（11·湖州）（本小题6分）计算：︱－2︱－2sin30°＋＋

（11·湖州）（本小题6分）因式分解：a³－9a

（11·湖州）（本小题6分）
已知：一次函数y=kx＋b的图象经过M（0，2），（1，3）两点。
⑴求k，b的值；
⑵若一次函数y=kx＋b的图象与x轴交点为A（a，0），求a的值。

（11·湖州）（本小题8分）
如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，∠AOC=60°，OC=2。
⑴求OE和CD的长；
⑵求图中阴影部队的面积。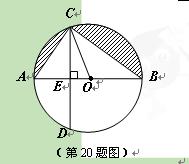

（11·湖州）（本小题8分）
班主任张老师为了了解学生课堂发言情况，对前一天本班男、女生发言次数进行了统计，并
绘制成如下频数分布折线图（图1）。
⑴请根据图1，回答下列问题：
①这个班共有 ▲ 名学生，发言次数是5次的男生有 ▲ 人、女生有 ▲ 人；
②男、女生发言次数的中位数分别是 ▲ 次和 ▲ 次；
⑵通过张老师的鼓励，第二天的发言次数比前一天明显增加，全班发言次数变化的人数的扇形统计图如图2所示，求第二天发言次数增加3次的学生人数和全班增加的发言总次数。

（11·湖州）（本小题10分）
如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF。
⑴求证：四边形AECF是平行四边形；
⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长。

（11·湖州）（本小题10分）
我市水产养殖专业户王大爷承包了30亩水塘，分别养殖甲鱼和桂鱼，有关成本、销售情况如下表：

⑴2010年，王大爷养殖甲鱼20亩，桂鱼10亩，求王大爷这一年共收益多少万元？（收益=销售额－成本）
⑵2011年，王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼，计划投入成本不超过70万元。若每亩养殖的成本、销售额与2010年相同，要获得最大收益，他应养殖甲鱼和桂鱼各多少亩？
⑶已知甲鱼每亩需要饲料500㎏，桂鱼每亩需要饲料700㎏，根据⑵中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍，结果运输养殖所需要全部饲料比原计划减少了2次，求王大爷原定的运输车辆每次可装载饲料多少㎏？

（11·湖州）（本小题？分）
如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点。P（0，m）是线段OC上一动点（C点除外），直线PM交AB的延长线于点D。
⑴求点D的坐标（用含m的代数式表示）；
⑵当△APD是等腰三角形时，求m的值；
⑶设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2），当点P从点O向点C运动时，点H也随之运动。请直接写出点H所经过的路径长。（不必写解答过程）