（11·湖州）（本小题10分）
如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF。
⑴求证：四边形AECF是平行四边形；
⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长。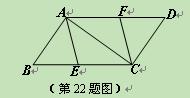
相关试题
.
，求代数式
的值．
与经过点A、D、B的抛物线的一部分
组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C的坐标为（0，
），点M是抛物线
的顶点．
的面积最大？若存在，求出
为直角三角形时，直接写出m的值．______相关知识点
推荐套卷
（11·湖州）（本小题10分）
如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF。
⑴求证：四边形AECF是平行四边形；
⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长。
粤公网安备 44130202000953号