（11·湖州）（本小题？分）
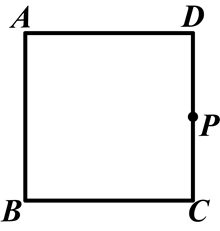
如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点。P（0，m）是线段OC上一动点（C点除外），直线PM交AB的延长线于点D。
⑴求点D的坐标（用含m的代数式表示）；
⑵当△APD是等腰三角形时，求m的值；
⑶设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2），当点P从点O向点C运动时，点H也随之运动。请直接写出点H所经过的路径长。（不必写解答过程）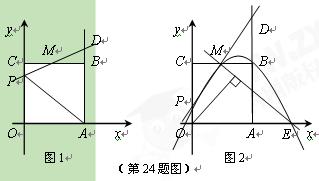
相关试题
的外接圆，
， 
为⊙O的直径，BD=2，连结
，求BC的长. 
，点B为CD延长线上一点，且BD＝2AD．求AB的长.
已知二次函数
（1）用配方法将
化成
的形式；（2）在坐标系中利用描点法画出它的图象；
| x |
… |
… |
|||||
| y |
… |
… |
（3）根据图象回答：当自变量x的取值范围满足什么
条件时，
随着
的增大而减小？
与
轴的两个交点分别为A、B,点A在点B的左侧，与y轴交于点C，顶点为D，直线
经过点A、C．
为抛物线上的一个动点，求使得
的面积与
的面积相等的点相关知识点
推荐套卷
粤公网安备 44130202000953号