初中数学平行四边形的判定与性质试题

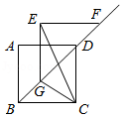
能够完全重合的平行四边形纸片 $\mathit{ABCD}$ 和 $\mathit{AEFG}$ 按图①方式摆放，其中 $\mathit{AD}=\mathit{AG}=5$ ， $\mathit{AB}=9$ ．点 $D$ ， $G$ 分别在边 $\mathit{AE}$ ， $\mathit{AB}$ 上， $\mathit{CD}$ 与 $\mathit{FG}$ 相交于点 $H$ ．

【探究】求证：四边形 $\mathit{AGHD}$ 是菱形．

【操作一】固定图①中的平行四边形纸片 $\mathit{ABCD}$ ，将平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 顺时针旋转一定的角度，使点 $F$ 与点 $C$ 重合，如图②．则这两张平行四边形纸片未重叠部分图形的周长和为 　    　．

【操作二】将图②中的平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 继续顺时针旋转一定的角度，使点 $E$ 与点 $B$ 重合，连接 $\mathit{DG}$ ， $\mathit{CF}$ ，如图③，若 $\sin \angle \mathit{BAD}=\frac{4}{5}$ ，则四边形 $\mathit{DCFG}$ 的面积为 　　．

如图，在中，点、分别在、上，与相交于点，且．

（1）求证：；

（2）连接、，则四边形　 　（填“是”或“不是” 平行四边形．

如图，在中，，，、分别是、的中点，连接，在直线和直线上分别取点、，连接、．若，且直线与直线互相垂直，则的长为　   　．

如图所示，点、分别是的边、的中点，连接，过点作，交的延长线于点，若，则的长为　　．

如图，点 $E$ ， $F$ 在 $▱\mathit{ABCD}$ 的边 $\mathit{BC}$ ， $\mathit{AD}$ 上， $\mathit{BE}=\frac{1}{3}\mathit{BC}$ ， $\mathit{FD}=\frac{1}{3}\mathit{AD}$ ，连接 $\mathit{BF}$ ， $\mathit{DE}$ ．

求证：四边形 $\mathit{BEDF}$ 是平行四边形．

如图，已知抛物线 $y=a{x}^2$ 过点 $A(-3,\frac{9}{4})$ ．

（1）求抛物线的解析式；

（2）已知直线 $l$ 过点 $A$ ， $M(\frac{3}{2}$ ， $0)$ 且与抛物线交于另一点 $B$ ，与 $y$ 轴交于点 $C$ ，求证： $M{C}^2=\mathit{MA}·\mathit{MB}$ ；

（3）若点 $P$ ， $D$ 分别是抛物线与直线 $l$ 上的动点，以 $\mathit{OC}$ 为一边且顶点为 $O$ ， $C$ ， $P$ ， $D$ 的四边形是平行四边形，求所有符合条件的 $P$ 点坐标．

九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究了函数 $y=\frac{2}{\left|x\right|}$ 的图象与性质共探究过程如下：

（1）绘制函数图象，如图1．

列表：下表是 $x$ 与 $y$ 的几组对应值，其中 $m=$ 　　；

$x$	$\dots$	$-3$	$-2$	$-1$	$-\frac{1}{2}$	$\frac{1}{2}$	1	2	3	$\dots$
$y$	$\dots$	$\frac{2}{3}$	1	2	4	4	2	$m$	$\frac{2}{3}$	$\dots$

描点：根据表中各组对应值 $(x,y)$ ，在平面直角坐标系中描出了各点；

连线：用平滑的曲线顺次连接各点，画出了部分图象．请你把图象补充完整；

（2）通过观察图1，写出该函数的两条性质；

① 　　；

② 　　；

（3）①观察发现：如图2．若直线 $y=2$ 交函数 $y=\frac{2}{\left|x\right|}$ 的图象于 $A$ ， $B$ 两点，连接 $\mathit{OA}$ ，过点 $B$ 作 $\mathit{BC}//\mathit{OA}$ 交 $x$ 轴于 $C$ ．则 $S_{\mathit{四边形}\mathit{OABC}}=$ 　　；

②探究思考：将①中"直线 $y=2$ "改为"直线 $y=a(a>0)$ "，其他条件不变，则 $S_{\mathit{四边形}\mathit{OABC}}=$ 　　；

③类比猜想：若直线 $y=a(a>0)$ 交函数 $y=\frac{k}{\left|x\right|}(k>0)$ 的图象于 $A$ ， $B$ 两点，连接 $\mathit{OA}$ ，过点 $B$ 作 $\mathit{BC}//\mathit{OA}$ 交 $x$ 轴于 $C$ ，则 $S_{\mathit{四边形}\mathit{OABC}}=$ 　　．

如图， $\mathit{AE}//\mathit{BF}$ ， $\mathit{BD}$ 平分 $\angle \mathit{ABC}$ 交 $\mathit{AE}$ 于点 $D$ ，点 $C$ 在 $\mathit{BF}$ 上且 $\mathit{BC}=\mathit{AB}$ ，连接 $\mathit{CD}$ ．求证：四边形 $\mathit{ABCD}$ 是菱形．

如图，在平行四边形中，对角线与交于点，点，分别为、的中点，延长至点，使，连接．

（1）求证：；

（2）若，且，，求四边形的面积．

如图，四边形是矩形，是边上一点，点在的延长线上，且．

（1）求证：四边形是平行四边形；

（2）连接，若，，，求四边形的面积．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\mathit{CD}$ 为斜边 $\mathit{AB}$ 的中线，过点 $D$ 作 $\mathit{DE}\perp \mathit{AC}$ 于点 $E$ ，延长 $\mathit{DE}$ 至点 $F$ ，使 $\mathit{EF}=\mathit{DE}$ ，连接 $\mathit{AF}$ ， $\mathit{CF}$ ，点 $G$ 在线段 $\mathit{CF}$ 上，连接 $\mathit{EG}$ ，且 $\angle \mathit{CDE}+\angle \mathit{EGC}=180°$ ， $\mathit{FG}=2$ ， $\mathit{GC}=3$ ．下列结论：

① $\mathit{DE}=\frac{1}{2}\mathit{BC}$ ；

②四边形 $\mathit{DBCF}$ 是平行四边形；

③ $\mathit{EF}=\mathit{EG}$ ；

④ $\mathit{BC}=2\sqrt{5}$ ．

其中正确结论的个数是 $($ 　　 $)$

A．

1个

B．

2个

C．

3个

D．

4个

如图，在边长为4的正方形中，将沿射线平移，得到，连接、．求的最小值为　　．

如图，在四边形中，连接，．请你添加一个条件　　，使．（填一种情况即可）

如图，在矩形中，为对角线的中点，过点作直线分别与矩形的边，交于，两点，连接，．

（1）求证：四边形为平行四边形；

（2）若，，且，求的长．

已知：点 $D$ ， $E$ 分别是 $\mathit{\Delta ABC}$ 的边 $\mathit{AB}$ ， $\mathit{AC}$ 的中点，如图所示．

求证： $\mathit{DE}//\mathit{BC}$ ，且 $\mathit{DE}=\frac{1}{2}\mathit{BC}$ ．

证明：延长 $\mathit{DE}$ 到点 $F$ ，使 $\mathit{EF}=\mathit{DE}$ ，连接 $\mathit{FC}$ ， $\mathit{DC}$ ， $\mathit{AF}$ ，又 $\mathit{AE}=\mathit{EC}$ ，则四边形 $\mathit{ADCF}$ 是平行四边形，接着以下是排序错误的证明过程：

① $\therefore \mathit{DF}\underset{=}{//}\mathit{BC}$ ；

② $\therefore \mathit{CF}\underset{=}{//}\mathit{AD}$ ．即 $\mathit{CF}\underset{=}{//}\mathit{BD}$ ；

③ $\therefore$ 四边形 $\mathit{DBCF}$ 是平行四边形；

④ $\therefore \mathit{DE}//\mathit{BC}$ ，且 $\mathit{DE}=\frac{1}{2}\mathit{BC}$ ．

则正确的证明顺序应是： $($ 　　 $)$

A．

② $\to$ ③ $\to$ ① $\to$ ④

B．

② $\to$ ① $\to$ ③ $\to$ ④

C．

① $\to$ ③ $\to$ ④ $\to$ ②

D．

① $\to$ ③ $\to$ ② $\to$ ④