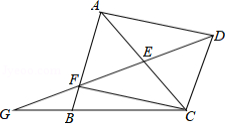
如图,在 中,过点 作 , 是 的中点,连接 并延长,交 于点 ,交 的延长线于点 ,连接 , .
(1)求证:四边形 是平行四边形.
(2)若 , , ,求 的长.
如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于 cm.

如图,在平行四边形ABCD中,延长AD到点E,使 ,连接EB,EC,DB请你添加一个条件 ,使四边形DBCE是矩形.

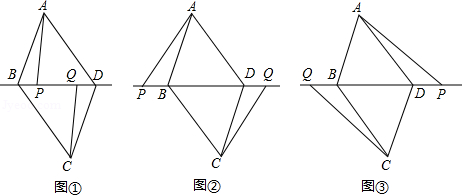
在▱ABCD中,点P和点Q是直线BD上不重合的两个动点, ,AD=BD.
(1)如图①,求证: ;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若 , ,则BC= .
爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线, 于点P,像△ABC这样的三角形均为“中垂三角形”.设 .
【特例探究】
(1)如图1,当 , 时,a= ,b= ;
如图2,当 , 时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且 ,连接AF、BE、CE,且 于E,AF与BE相交点G, , ,求AF的长.

如图,在△ABC中, ,M、N分别是AB、AC的中点,延长BC至点D,使 ,连接DM、DN、MN.若AB=6,则DN= .

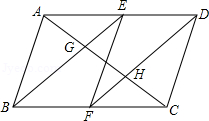
如图,在▱ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
如图,▱ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长.

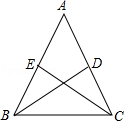
如图,等腰三角形 ABC中, BD, CE分别是两腰上的中线.
(1)求证: BD= CE;
(2)设 BD与 CE相交于点 O,点 M, N分别为线段 BO和 CO的中点,当△ ABC的重心到顶点 A的距离与底边长相等时,判断四边形 DEMN的形状,无需说明理由.
如图,在四边形 中,
中, ,
, 是
是 中点,
中点, 于点
于点 ,
, ,
, .
.
(1)若 ,则四边形
,则四边形 的面积
的面积 ;
;
(2)若 ,则此时四边形
,则此时四边形 的面积
的面积
 (用“
(用“ ”或“
”或“ ”或“
”或“ ”填空).
”填空).

在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )

A.5B.7C.9D.11
如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF
(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.

如图,利用尺规,在△ ABC的边 AC上方作∠ CAE=∠ ACB,在射线 AE上截取 AD= BC,连接 CD,并证明: CD∥ AB(尺规作图要求保留作图痕迹,不写作法)
