如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

在① ;② ;③ 这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知,如图,四边形 是平行四边形,对角线 、 相交于点 ,点 、 在 上, (填写序号).
求证: .

如图,点 是 的中点,四边形 是平行四边形.
(1)求证:四边形 是平行四边形;
(2)如果 ,求证:四边形 是矩形.
如图所示,在矩形 中,点 在线段 上,点 在线段 的延长线上,连接 交线段 于点 ,连接 ,若 .
(1)求证:四边形 是平行四边形;
(2)若 ,求线段 的长度.

如图,在四边形 中, , ,垂足分别为点 , .
(1)请你只添加一个条件(不另加辅助线),使得四边形 为平行四边形,你添加的条件是 ;
(2)添加了条件后,证明四边形 为平行四边形.

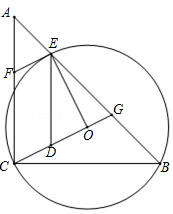
如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , .
(1)求证: 是直角三角形;
(2)求证: ;
(3)当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.

【基础巩固】
(1)如图1,在 中, 为 上一点, .求证: .
【尝试应用】
(2)如图2,在 中, 为 上一点, 为 延长线上一点, .若 , ,求 的长.
【拓展提高】
(3)如图3,在菱形 中, 是 上一点, 是 内一点, , , , , ,求菱形 的边长.

如图,矩形 中, 是 的中点,延长 , 交于点 ,连接 , .
(1)求证:四边形 是平行四边形;
(2)当 平分 时,写出 与 的数量关系,并说明理由.

已知在 中, , , , 分别为 , 边上的点(不包括端点),且 ,连接 ,过点 作 ,垂足为点 ,延长 交 于点 .
(1)如图1,过点 作 于点 ,连接 .
①求证:四边形 是平行四边形;
②若 ,求证: ;
(2)如图2,若 ,求 的值.

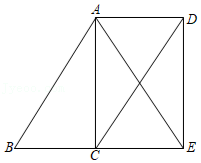
如图,在 中, , , (圆心 在 内部)经过 、 两点,交 于点 ,过点 作 的切线交 于点 .延长 交 于点 ,作 交 于点
(1)求证:四边形 是平行四边形;
(2)若 , ,求 的值.
如图, 是 的中线, 是线段 上一点(不与点 重合). 交 于点 , ,连接 .
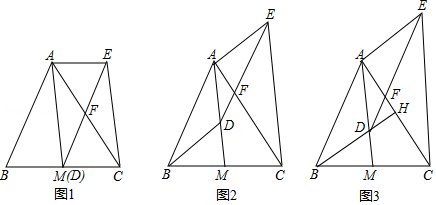
(1)如图1,当点 与 重合时,求证:四边形 是平行四边形;
(2)如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 交 于点 ,若 ,且 .
①求 的度数;
②当 , 时,求 的长.