如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .

如图,在 中,点 在 的延长线上,点 在 的延长线上,满足 .连接 ,分别与 , 交于点 , .
求证: .

已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

请认真阅读下面的数学小探究系列,完成所提出的问题:
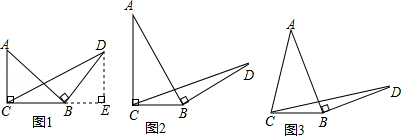
(1)探究1:如图1,在等腰直角三角形 中, , ,将边 绕点 顺时针旋转 得到线段 ,连接 .求证: 的面积为 .(提示:过点 作 边上的高 ,可证 )
(2)探究2:如图2,在一般的 中, , ,将边 绕点 顺时针旋转 得到线段 ,连接 .请用含 的式子表示 的面积,并说明理由.
(3)探究3:如图3,在等腰三角形 中, , ,将边 绕点 顺时针旋转 得到线段 ,连接 .试探究用含 的式子表示 的面积,要有探究过程.
如图,在平行四边形 中, 为 边上的中点,连接 并延长,交 的延长线于点 .
(1)求证: ;
(2)若平行四边形 的面积为32,试求四边形 的面积.

如图,在平面直角坐标系中,一次函数 的图象与 轴、 轴分别相交于点 ,点 ,以线段 为边作正方形 ,且点 在反比例函数 的图象上,则 的值为

| A. |
|
B. |
|
C. |
42 |
D. |
|
正方形 的边长为 ,点 、 分别是线段 、 上的动点,连接 并延长,交边 于 ,过 作 ,垂足为 ,交边 于点 .

(1)如图1,若点 与点 重合,求证: ;
(2)如图2,若点 从点 出发,以 的速度沿 向点 运动,同时点 从点 出发,以 的速度沿 向点 运动,运动时间为 .
①设 ,求 关于 的函数表达式;
②当 时,连接 ,求 的长.
如图, 是 的边 的中点,延长 交 的延长线于点 .
(1)求证: .
(2)若 , , ,求 的长.

如图放置的两个正方形,大正方形 边长为 ,小正方形 边长为 , 在 边上,且 ,连接 , , 交 于点 ,将 绕点 旋转至 ,将 绕点 旋转至 ,给出以下五个结论:① ;② ;③ ;④ ;⑤ , , , 四点共圆,其中正确的个数是

A.2B.3C.4D.5
如图,在四边形中,
,点
是对角线
的中点,过点
作
的垂线,分别交
、
于点
、
,连接
、
.试判断四边形
的形状,并证明.

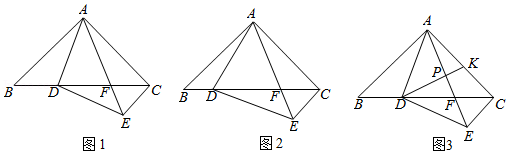
在 中, , ,点 在边 上, 且 , 交边 于点 ,连接 .
(1)特例发现:如图1,当 时,
①求证: ;
②推断: ;
(2)探究证明:如图2,当 时,请探究 的度数是否为定值,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,当 时,过点 作 的垂线,交 于点 ,交 于点 ,若 ,求 的长.
如图,在四边形 中, , ,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形 的对角线 , 相交于点 .以点 为圆心, 长为半径画弧,分别交 , 于点 , .若 , ,则 的长为 (结果保留 .
