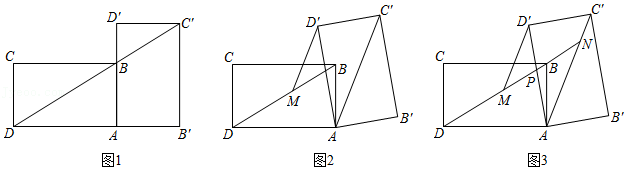
小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形 绕点 顺时针旋转 ,得到矩形 ,连结 .
探究 如图1,当 时,点 恰好在 延长线上.若 ,求 的长.
探究 如图2,连结 ,过点 作 交 于点 .线段 与 相等吗?请说明理由.
探究 在探究2的条件下,射线 分别交 , 于点 , (如图 ,发现线段 , , 存在一定的数量关系,请写出这个关系式,并加以证明.
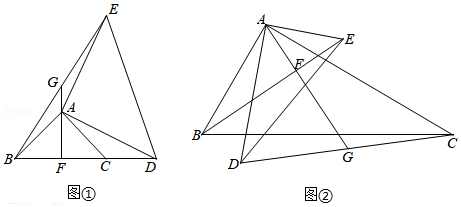
(1)已知 , 如图①摆放,点 , , 在同一条直线上, , .连接 ,过点 作 ,垂足为点 ,直线 交 于点 .求证: .
(2)已知 , 如图②摆放, , .连接 , ,过点 作 ,垂足为点 ,直线 交 于点 .求 的值.
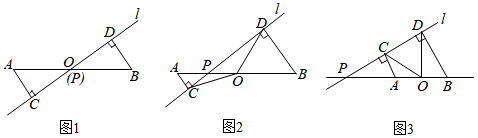
已知点 是线段 的中点,点 是直线 上的任意一点,分别过点 和点 作直线 的垂线,垂足分别为点 和点 .我们定义垂足与中点之间的距离为"足中距".
(1) 猜想验证 如图1,当点 与点 重合时,请你猜想、验证后直接写出"足中距" 和 的数量关系是 .
(2) 探究证明 如图2,当点 是线段 上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3) 拓展延伸 如图3,①当点 是线段 延长线上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若 ,请直接写出线段 、 、 之间的数量关系.
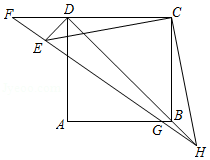
已知四边形 是边长为1的正方形,点 是射线 上的动点,以 为直角边在直线 的上方作等腰直角三角形 , ,设 .
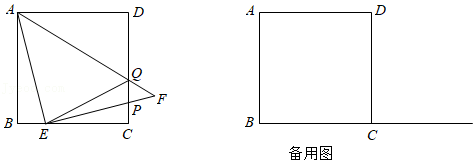
(1)如图,若点 在线段 上运动, 交 于点 , 交 于点 ,连结 ,
①当 时,求线段 的长;
②在 中,设边 上的高为 ,请用含 的代数式表示 ,并求 的最大值;
(2)设过 的中点且垂直于 的直线被等腰直角三角形 截得的线段长为 ,请直接写出 与 的关系式.
在数学兴趣小组活动中,小亮进行数学探究活动.
(1) 是边长为3的等边三角形, 是边 上的一点,且 ,小亮以 为边作等边三角形 ,如图1.求 的长;

(2) 是边长为3的等边三角形, 是边 上的一个动点,小亮以 为边作等边三角形 ,如图2.在点 从点 到点 的运动过程中,求点 所经过的路径长;
(3) 是边长为3的等边三角形, 是高 上的一个动点,小亮以 为边作等边三角形 ,如图3.在点 从点 到点 的运动过程中,求点 所经过的路径长;

(4)正方形 的边长为3, 是边 上的一个动点,在点 从点 到点 的运动过程中,小亮以 为顶点作正方形 ,其中点 、 都在直线 上,如图4.当点 到达点 时,点 、 、 与点 重合.则点 所经过的路径长为 ,点 所经过的路径长为 .
如图1,在 中, , 是 边上的一点, 为 的中点,过点 作 的平行线交 的延长线于 ,且 ,连接 .
(1)求证: ;
(2)在图1中 上取一点 ,使 ,作 关于边 的对称点 ,连接 、 、 、 、 得图2.
①求证: ;
②设 与 相交于点 ,求证: , .

如图所示,四边形 为正方形,在 中, , , 的延长线与 的延长线交于点 ,点 、 、 在同一条直线上.
(1)求证: ;
(2)当 时,求 的值;
(3)当 , 时,求 的值.
下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段,请仔细阅读,并完成相应的任务.
小明:如图1, 分别在射线OA,OB上截取 , 点C,E不重合 ; 分别作线段CE,DF的垂直平分线 , ,交点为P,垂足分别为点G,H; 作射线OP,射线即为 的平分线. 简述理由如下: 由作图知, , , ,所以 ≌ ,则 ,即射线OP是 的平分线. 小军:我认为小明的作图方法很有创意,但是太麻烦了,可以改进如下,如图2, 分别在射线OA,OB上截取 , 点C,E不重合 ; 连接DE,CF,交点为P; 作射线 射线OP即为 的平分线.
|
任务:

小明得出 ≌ 的依据是______ 填序号 .
小军作图得到的射线0P是 的平分线吗?请判断并说明理由.
如图3,已知 ,点E,F分别在射线OA,OB上,且 点C,D分别为射线OA,OB上的动点,且 ,连接DE,CF,交点为P,当 时,直接写出线段OC的长.