如图放置的两个正方形,大正方形 边长为 ,小正方形 边长为 , 在 边上,且 ,连接 , , 交 于点 ,将 绕点 旋转至 ,将 绕点 旋转至 ,给出以下五个结论:① ;② ;③ ;④ ;⑤ , , , 四点共圆,其中正确的个数是
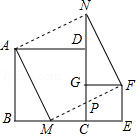
A.2B.3C.4D.5
相关知识点
推荐套卷
如图放置的两个正方形,大正方形 边长为 ,小正方形 边长为 , 在 边上,且 ,连接 , , 交 于点 ,将 绕点 旋转至 ,将 绕点 旋转至 ,给出以下五个结论:① ;② ;③ ;④ ;⑤ , , , 四点共圆,其中正确的个数是

A.2B.3C.4D.5