如图,正方形 的对角线 , 相交于点 , , 为 上一点, ,连接 ,过点 作 于点 ,与 交于点 ,则 的长是

A. B. C. D.
如图,四边形 ABCD是正方形,点 E是 BC的中点,∠ AEF=90°, EF交正方形外角的平分线 CF于 F.求证: AE= EF.

已知:在四边形 中,对角线 、 相交于点 ,且 ,作 ,垂足为点 , 与 交于点 , .
(1)如图1,求证: ;
(2)如图2, 是 的中线,若 , ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于 面积的2倍.

如图,正方形 ABCD的边长为3 cm, P, Q分别从 B, A出发沿 BC, AD方向运动, P点的运动速度是1 cm/秒, Q点的运动速度是2 cm/秒,连接 A, P并过 Q作 QE⊥ AP垂足为 E.
(1)求证:△ ABP∽△ QEA;
(2)当运动时间 t为何值时,△ ABP≌△ QEA;
(3)设△ QEA的面积为 y,用运动时刻 t表示△ QEA的面积 y(不要求考 t的取值范围).(提示:解答(2)(3)时可不分先后)

如图,在△ ABC中,∠ C=90°,∠ ABC的平分线交 AC于点 E,过点 E作 BE的垂线交 AB于点 F,⊙ O是△ BEF的外接圆.
(1)求证: AC是⊙ O的切线;
(2)过点 E作 EH⊥ AB,垂足为 H,求证: CD= HF;
(3)若 CD=1, EH=3,求 BF及 AF长.
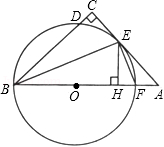
如图, 是 的直径,点 为线段 上一点(不与 , 重合),作 ,交 于点 ,作直径 ,过点 的切线交 的延长线于点 ,作 于点 ,连接 .
(1)求证: 平分 ;
(2)求证: ;
(3)当 且 时,求劣弧 的长度.

正方形 的边长为 ,点 、 分别是线段 、 上的动点,连接 并延长,交边 于 ,过 作 ,垂足为 ,交边 于点 .

(1)如图1,若点 与点 重合,求证: ;
(2)如图2,若点 从点 出发,以 的速度沿 向点 运动,同时点 从点 出发,以 的速度沿 向点 运动,运动时间为 .
①设 ,求 关于 的函数表达式;
②当 时,连接 ,求 的长.
如图, 是 的边 的中点,延长 交 的延长线于点 .
(1)求证: .
(2)若 , , ,求 的长.

如图放置的两个正方形,大正方形 边长为 ,小正方形 边长为 , 在 边上,且 ,连接 , , 交 于点 ,将 绕点 旋转至 ,将 绕点 旋转至 ,给出以下五个结论:① ;② ;③ ;④ ;⑤ , , , 四点共圆,其中正确的个数是

A.2B.3C.4D.5
如图,在边长为的菱形
中,
,点
,
分别是
,
上的动点,且
,
与
交于点
.当点
从点
运动到点
时,则点
的运动路径长为 .
如图,点,
,
,
在一条直线上,
,
,
.
(1)求证:;
(2)连接,求证:四边形
是平行四边形.

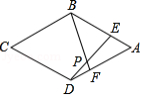
如图,在菱形 中, ,点 , 分别在 , 上,且 , 与 相交于点 , 与 相交于点 .下列结论:① ;② ;③若 ,则 ;④ .其中正确的结论有 .(只填序号即可)

如图,正方形 , 是 边上任意一点(不与 、 重合), 于点 , ,且交 于点 .
(1)求证: ;
(2)四边形 是否可能是平行四边形,如果可能,请指出此时点 的位置,如不可能,请说明理由.
