平面直角坐标系 中,横坐标为 的点 在反比例函数 的图象上,点 与点 关于点 对称,一次函数 的图象经过点 .
(1)设 ,点 在函数 、 的图象上.
①分别求函数 、 的表达式;
②直接写出使 成立的 的范围;
(2)如图①,设函数 、 的图象相交于点 ,点 的横坐标为 ,△ 的面积为16,求 的值;
(3)设 ,如图②,过点 作 轴,与函数 的图象相交于点 ,以 为一边向右侧作正方形 ,试说明函数 的图象与线段 的交点 一定在函数 的图象上.

如图,直线 与 , 轴分别交于点 , ,与反比例函数 图象交于点 , ,过点 作 轴的垂线交该反比例函数图象于点 .
(1)求点 的坐标.
(2)若 .
①求 的值.
②试判断点 与点 是否关于原点 成中心对称?并说明理由.

如图, ,反比例函数 的图象过点 ,反比例函数 的图象过点 ,且 轴.
(1)求 和 的值;
(2)过点 作 ,交 轴于点 ,交 轴于点 ,交双曲线 于另一点 ,求 的面积.
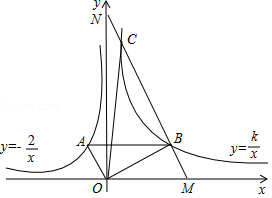
如图,点 和点 是反比例函数 图象上的两点,一次函数 的图象经过点 ,与 轴交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,连接 , .已知 与 的面积满足 .
(1) , ;
(2)已知点 在线段 上,当 时,求点 的坐标.

如图,已知菱形 的对称中心是坐标原点 ,四个顶点都在坐标轴上,反比例函数 的图象与 边交于 , 两点.
(1)求 , 的值;
(2)写出函数 图象在菱形 内 的取值范围.

已知反比例函数的图象经过三个点 , , ,其中 .
(1)当 时,求 的值;
(2)如图,过点 、 分别作 轴、 轴的垂线,两垂线相交于点 ,点 在 轴上,若三角形 的面积是8,请写出点 坐标(不需要写解答过程).
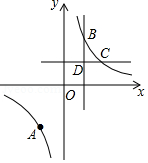
如图,在平面直角坐标系中, 的斜边 在 轴的正半轴上, ,且 , ,反比例函数 的图象经过点 .
(1)求反比例函数的表达式;
(2)若 与 关于直线 对称,一次函数 的图象过点 、 ,求一次函数的表达式.
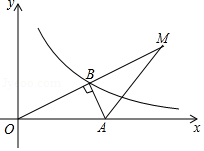
如图1,一次函数 的图象与 轴交于点 ,与反比例函数 的图象交于点 .
(1) ; ;
(2)点 是线段 上的动点(与点 、 不重合),过点 且平行于 轴的直线 交这个反比例函数的图象于点 ,求 面积的最大值;
(3)将(2)中面积取得最大值的 沿射线 方向平移一定的距离,得到△ ,若点 的对应点 落在该反比例函数图象上(如图 ,则点 的坐标是 .

如图,四边形 是矩形,点 在第四象限 的图象上,点 在第一象限 的图象上, 交 轴于点 ,点 与点 在 轴上, , .
(1)求点 的坐标.
(2)若点 在 轴上, ,求直线 的解析式.
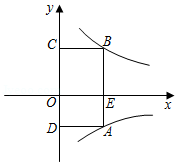
如图,在平面直角坐标系中,矩形 的边 交 轴于点 , 轴,反比例函数 的图象经过点 ,点 的坐标为 , .
(1)求反比例函数的解析式;
(2)点 为 轴上一动点,当 的值最小时,求出点 的坐标.

如图,一次函数 的图象与反比例函数 的图象在第二象限交于点 .与 轴交于点 .过点 作 轴于点 , 的面积是3.
(1)求一次函数和反比例函数的解析式;
(2)若直线 与 轴交于点 ,求 的面积.

如图,在平面直角坐标系中有三点 , , ,其中有两点同时在反比例函数 的图象上,将这两点分别记为 , ,另一点记为 .
(1)求出 的值;
(2)求直线 对应的一次函数的表达式;
(3)设点 关于直线 的对称点为 , 是 轴上的一个动点,直接写出 的最小值(不必说明理由).
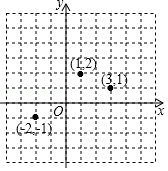
如图,已知反比例函数 的图象经过点 , 轴,且 的面积为2.
(1)求 和 的值;
(2)若点 也在反比例函数 的图象上,当 时,求函数值 的取值范围.

一个不透明的口袋中有三个完全相同的小球,球上分别标有数字 ,1,2.第一次从袋中任意摸出一个小球(不放回),得到的数字作为点 的横坐标 ;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点 的纵坐标 .
(1)用列表法或树状图法,列出点 的所有可能结果;
(2)求点 在双曲线 上的概率.