高中数学试题

设有下面四个命题

$p_1$ ：若复数 $z$ 满足 $\frac{1}{z}\in R$ ，则 $z\in R$ ；

$p_2$ ：若复数 $z$ 满足 $z^2\in R$ ，则 $z\in R$ ；

$p_3$ ：若复数 $z_1,z_2$ 满足 $z_1{z}_2\in R$ ，则 $z_1=\overline{z_2}$ ；

$p_4$ ：若复数 $z\in R$ ，则 $\bar{z}\in R$ .

其中的真命题为(    )

A．

$p_1,p_3$

B．

$p_1,p_4$

C．

$p_2,p_3$

D．

$p_2,p_4$

如图，正方形 ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是（ ）

A．	$\frac{1}{4}$	B．	$\frac{\pi }{8}$
C．	$\frac{1}{2}$	D．	$\frac{\pi }{4}$

已知集合 $A=\left\{x\right|x<1\}$ ， $B=\left\{x\right|3^x<1$ }，则（ ）

A．	$A\cap B=\left\{x\right|x<0\}$	B．	$A\cup B=R$
C．	$A\cup B=\left\{x\right|x>1\}$	D．	$A\cap B=\varnothing$

[选修4-5：不等式选讲]

已知函数 $f（x）=\left|2x﹣a\right|+a$ ．

（1）当 $a=2$ 时，求不等式 $f（x）\le 6$ 的解集；

（2）设函数 $g（x）=\left|2x﹣1\right|$ ，当 $x\in R$ 时， $f（x）+g（x）\ge 3$ ，求a的取值范围．

[选修4-4：坐标系与参数方程]

在直角坐标系 $\mathit{xOy}$ 中，曲线 $C_1$ 的参数方程为 $\left\{\begin{array}{c}x=\sqrt{3}\cos \alpha \\ y=\sin \alpha \end{array}\right.（\alpha \mathrm{为参数}）$ ，以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线 $C_2$ 的极坐标方程为 $\mathit{\rho sin}（\theta +\frac{\pi }{4}）=2\sqrt{2}$ ．

（1）写出 $C_1$ 的普通方程和 $C_2$ 的直角坐标方程；

（2）设点P在 $C_1$ 上，点Q在 $C_2$ 上，求 $\left|\mathit{PQ}\right|$ 的最小值及此时P的直角坐标．

[选修4-1：几何证明选讲]如图，⊙O中 $\stackrel{̂}{\mathit{AB}}$的中点为P，弦PC，PD分别交AB于E，F两点．

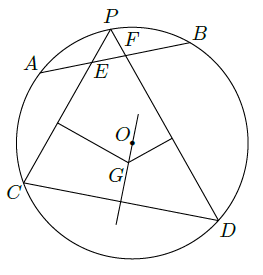
（1）若 $\angle \mathit{PFB}=2\angle \mathit{PCD}$，求 $\angle \mathit{PCD}$的大小；

（2）若EC的垂直平分线与FD的垂直平分线交于点G，证明： $\mathit{OG}\perp \mathit{CD}$．

设函数 $f（x）=\mathit{lnx}﹣x+1$．

（1）讨论 $f（x）$的单调性；

（2）证明当x∈（1，+∞）时，1＜ $\frac{x-1}{\ln x}$ ＜x；

（3）设c＞1，证明当x∈（0，1）时，1+（c﹣1）x＞c^x ．

已知抛物线 $C：y^2=2x$ 的焦点为F，平行于x轴的两条直线 $l_1$ ， $l_2$ 分别交C于A，B两点，交C的准线于P，Q两点．

（1）若F在线段AB上，R是PQ的中点，证明 $\mathit{AR}\parallel \mathit{FQ}$ ；

（2）若 $△\mathit{PQF}$ 的面积是 $△\mathit{ABF}$ 的面积的两倍，求AB中点的轨迹方程．

如图，四棱锥 $P﹣\mathit{ABCD}$ 中， $PA\mathit{\perp }\mathit{底面}\mathit{ABCD}$ ， $\mathit{AD}\parallel \mathit{BC}$ ， $\mathit{AB}=\mathit{AD}=\mathit{AC}=3$ ， $\mathit{PA}=\mathit{BC}=4$ ，M为线段AD上一点， $\mathit{AM}=2\mathit{MD}$ ，N为PC的中点．

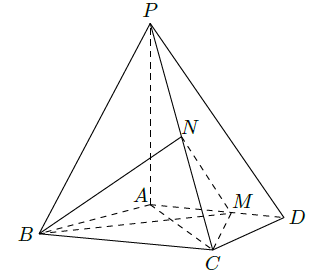
（1）证明 $\mathit{MN}\parallel \mathrm{平面}PAB$；

（2）求四面体 $N﹣\mathit{BCM}$ 的体积．

如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．

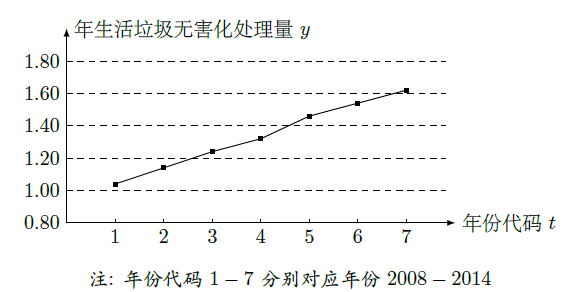
（1）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以证明；

（2）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．

附注：

参考数据： $\underset{i=1}{\overset{7}{\sum }}\mathrm{y}\mathrm{i}=9.32$ ， $\underset{i=1}{\overset{7}{\sum }}\mathrm{t}\mathrm{i}\mathrm{y}\mathrm{i}=40.17$ ， $\sqrt{\underset{i=1}{\overset{7}{\sum }}{\left(y_i-\stackrel{-}{y}\right)}^2}$ $=0.55$ ， $\sqrt{7}\approx 2.646$ ．

参考公式： $r=\frac{\underset{i=1}{\overset{7}{\sum }}\left(t_i-\stackrel{-}{t}\right)\left(y_i-\stackrel{-}{y}\right)}{\sqrt{\underset{i=1}{\overset{7}{\sum }}{\left(t_i-\stackrel{-}{t}\right)}^2\underset{i=1}{\overset{7}{\sum }}{\left(y_i-\stackrel{-}{y}\right)}^2}}$ ，回归方程 $\stackrel{\wedge }{y}=\stackrel{\wedge }{a}+\stackrel{\wedge }{b}t$ 中斜率和截距的最小二乘估计公式分别为：

$\stackrel{\wedge }{b}=\frac{\underset{i=1}{\overset{n}{\sum }}\left(t_i-\stackrel{-}{t}\right)\left(y_i-\stackrel{-}{y}\right)}{\underset{i=1}{\overset{n}{\sum }}{\left(t_i-\stackrel{-}{t}\right)}^2}$ ， $\stackrel{\wedge }{a}=\stackrel{-}{y}-\stackrel{\wedge }{b}\stackrel{-}{t}$ ．

已知各项都为正数的数列 $\left\{a_n\right\}$ 满足 $a_1=1$ ， $a_n^2\mathit{﹣（}2a_{n+1}﹣1）a_n﹣2a_{n+1}=0$

（1）求 $a_2\mathit{ }$ ， $a_3$ ；

（2）求 $\left\{a_n\right\}$ 的通项公式．

已知 $f\left(x\right)$ 为偶函数，当 $x\le 0$ 时， $f（x）=e^{﹣x﹣1}﹣x$ ，则曲线 $y=f\left(x\right)$ 在点 $\left(1，2\right)$ 处的切线方程是________．

已知直线 $l：x﹣\sqrt{3}y+6=0$与圆 $x^2+y^2=12$交于A，B两点，过A，B分别作l的垂线与x轴交于C，D两点．则|CD|=________．

函数 $y=\mathit{sinx}﹣\sqrt{3}\mathit{cosx}$的图象可由函数 $y=2\mathit{sinx}$的图象至少向右平移________个单位长度得到．

设x，y满足约束条件 $\left\{\begin{array}{c}2x-y+1\ge 0\\ x-2y-1\le 0\\ x\le 1\end{array}\right.$ ，则 $z=2x+3y﹣5$的最小值为________．