高中数学试题

已知函数 $f\left(x\right)={\cos }^{2}x-{\sin }^{2}x+\frac{1}{2},x\in \left(0,\mathrm{\pi }\right)$  ．    

（1）求 $f\left(x\right)$ 的单调递增区间；    

（2）设△ABC为锐角三角形，角A所对边 $a=\sqrt{19}$ ，角B所对边b=5，若 $f\left(A\right)=0$ ，求△ABC的面积．

如图，直三棱柱ABC﹣A ₁B ₁C ₁的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱 $A{A}_1$ 的长为5．

（1）求三棱柱ABC﹣A ₁B ₁C ₁的体积；    

（2）设M是BC中点，求直线A ₁M与平面ABC所成角的大小．    

在平面直角坐标系xOy中，已知椭圆C ₁： $\frac{x^2}{36}+\frac{y^2}{4}=1$  和C ₂： $x^2+\frac{y^2}{9}=1$ ．P为C ₁上的动点，Q为C ₂上的动点，w是 $\stackrel{\to }{OP}·\stackrel{\to }{OQ}$ 的最大值．记 $\Omega =\left\{\left(P,Q\right)\overline{)P}在C_1上,Q在C_2上,且\stackrel{\to }{OP}·\stackrel{\to }{OQ}=w\right\}$ ，则 $\Omega$ 中元素个数为（ ）            

A．

2个

B．

4个

C．

8个

D．

无穷个

已知a、b、c为实常数，数列 $\left\{x_n\right\}$ 的通项 ^{$x_n=a{n}^2+bn+c,n\in N^{*}$} ，则"存在k∈N ^*，使得x _100+k、x _200+k、x _300+k成等差数列"的一个必要条件是（ ）            

A．

$a\ge 0$

B．

$b\le 0$

C．

$c=0$

D．

$a-2b+c=0$

在数列 $\left\{a_n\right\}$ 中， $a_n={\left(-\frac{1}{2}\right)}^n,n\in N^{*}$ ，则 $\underset{n\to \infty }{\mathit{lim}}{a}_n$ （ ）            

A．

等于 $-\frac{1}{2}$

B．

等于0

C．

等于 $\frac{1}{2}$

D．

不存在

关于x、y的二元一次方程组 $\{\begin{array}{c}x+5y=0\\ 2x+3y=4\end{array}$ 的系数行列式D为（ ）            

A．

$\left|\begin{array}{cc}0& 5\\ 4& 3\end{array}\right|$

B．

$\left|\begin{array}{cc}1& 0\\ 2& 4\end{array}\right|$

C．

$\left|\begin{array}{cc}1& 5\\ 2& 3\end{array}\right|$

D．

$\left|\begin{array}{cc}6& 0\\ 5& 4\end{array}\right|$

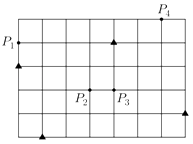
如图，用35个单位正方形拼成一个矩形，点P ₁、P ₂、P ₃、P ₄以及四个标记为"▲"的点在正方形的顶点处，设集合 $\Omega =\left\{P_1,P_2,P_3,P_4\right\}$ ，点P∈Ω，过P作直线l _P ， 使得不在l _P上的"▲"的点分布在l _P的两侧．用D ₁（l _P）和D ₂（l _P）分别表示l _P一侧和另一侧的"▲"的点到l _P的距离之和．若过P的直线l _P中有且只有一条满足D ₁（l _P）=D ₂（l _P），则Ω中所有这样的P为________．

设 $a_1$ 、 $a_2\in R$ ，且 $\frac{1}{2+\mathit{sin}{\alpha }_1}+\frac{1}{2+sin\left(2{\alpha }_2\right)}=2$ ，则 $\left|10\mathrm{\pi }-{\mathrm{a}}_1-{\mathrm{a}}_2\right|$ 的最小值等于________．    

已知数列 $\left\{a_n\right\}$ 和 $\left\{b_n\right\}$ ，其中 $a_n=n^2,n\in N^{*}$ ， $\left\{b_n\right\}$ 的项是互不相等的正整数，若对于任意 $n\in N^{*}$ ， $\left\{b_n\right\}$ 的第a _n项等于 $\left\{a_n\right\}$ 的第 $b_n$ 项，则 $\frac{\mathit{lg}\left(b_1{b}_4{b}_9{b}_{16}\right)}{\mathit{lg}\left(b_1{b}_2{b}_3{b}_4\right)}=$ ________．

已知四个函数：① $y=-x$ ，② $y=-\frac{1}{x}$ ，③ $y=x^3$ ， ④ ${y=x}^{\frac{1}{2}}$ ，从中任选2个，则事件"所选2个函数的图象有且仅有一个公共点"的概率为________．    

定义在 $\left(0,+\infty \right)$ 上的函数 $y=f\left(x\right)$ 的反函数为 $y=f^{-1}\left(x\right)$ ，若  $g\left(x\right)=\{\begin{array}{c}{3}^x-1，x\le 0\\ f\left(x\right)，x>0\end{array}$ 为奇函数，则 $f^{-1}\left(x\right)=2$ 的解为________．    

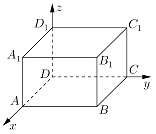
如图，以长方体ABCD﹣A ₁B ₁C ₁D ₁的顶点D为坐标原点，过D的三条棱所在的直线为坐标轴，建立空间直角坐标系，若 $\stackrel{\to }{D{B}_1}$ 的坐标为（4，3，2），则 $\stackrel{\to }{A{C}_1}$ 的坐标是________．

设双曲线 $\frac{x^2}{9}-\frac{y^2}{b^2}=1\left(b>0\right)$ 的焦点为F ₁、F ₂ ， P为该双曲线上的一点，若 $\left|P{F}_1\right|=5$ ，则 $\left|P{F}_2\right|=$ ________．    

已知复数z满足 $z+\frac{3}{z}=0$ ，则 $\left|z\right|$ =________．    

已知球的体积为 $36\mathrm{\pi }$ ，则该球主视图的面积等于________．