已知 F是双曲线 C: x 2 1的右焦点, P是 C上一点,且 PF与 x轴垂直,点 A的坐标是(1,3),则△ APF的面积为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,正方形 ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )

| A. |
|
B. |
|
C. |
|
D. |
|
下列各式的运算结果为纯虚数的是( )
| A. |
i(1+i) 2 |
B. |
i 2(1﹣i) |
C. |
(1+i) 2 |
D. |
i(1+i) |
为评估一种农作物的种植效果,选了 n块地作试验田.这 n块地的亩产量(单位: kg)分别是 x 1, x 2,…, x n,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
| A. |
x 1,x 2,…,x n的平均数 |
B. |
x 1,x 2,…,x n的标准差 |
| C. |
x 1,x 2,…,x n的最大值 |
D. |
x 1,x 2,…,x n的中位数 |
已知集合 A={ x| x<2}, B={ x|3﹣2 x>0},则( )
| A. |
A∩B={x|x } |
B. |
A∩B=∅ |
C. |
A∪B={x|x } |
D. |
A∪B=R |
设函数 f( x)=(1﹣ x 2) e x.
(1)讨论 f( x)的单调性;
(2)当 x≥0时, f( x)≤ ax+1,求 a的取值范围.
设 O为坐标原点,动点 M在椭圆 C: y 2=1上,过 M作 x轴的垂线,垂足为 N,点 P满足 .
(1)求点 P的轨迹方程;
(2)设点 Q在直线 x=﹣3上,且 • 1.证明:过点 P且垂直于 OQ的直线 l过 C的左焦点 F.
海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位: kg),其频率分布直方图如下:
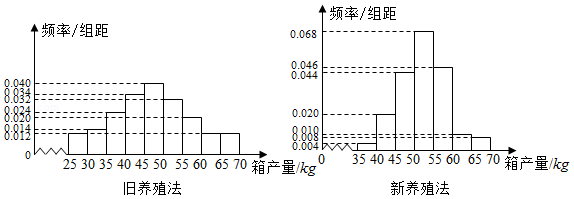
(1)记 A表示事件"旧养殖法的箱产量低于50 kg",估计 A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
| |
箱产量<50 kg |
箱产量≥50 kg |
| 旧养殖法 |
|
|
| 新养殖法 |
|
|
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
| P( K 2≥ K) |
0.050 |
0.010 |
0.001 |
| K |
3.841 |
6.635 |
10.828 |
K 2 .
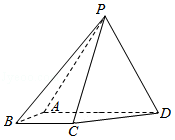
如图,四棱锥 P﹣ ABCD中,侧面 PAD为等边三角形且垂直于底面 ABCD, AB= BC AD,∠ BAD=∠ ABC=90°.
(1)证明:直线 BC∥平面 PAD;
(2)若△ PCD面积为2 ,求四棱锥 P﹣ ABCD的体积.
已知等差数列{ a n}的前 n项和为 S n,等比数列{ b n}的前 n项和为 T n, a 1=﹣1, b 1=1, a 2+ b 2=2.
(1)若 a 3+ b 3=5,求{ b n}的通项公式;
(2)若 T 3=21,求 S 3.
△ ABC的内角 A, B, C的对边分别为 a, b, c,若2 bcos B= acos C+ ccos A,则 B= .
长方体的长、宽、高分别为3,2,1,其顶点都在球 O的球面上,则球 O的表面积为 .
已知函数 f( x)是定义在 R上的奇函数,当 x∈(﹣∞,0)时, f( x)=2 x 3+ x 2,则 f(2)= .