安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
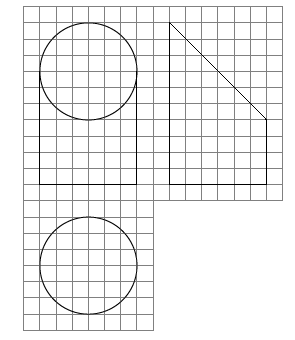
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
| A. |
|
B. |
|
C. |
|
D. |
|
我国古代数学名著《算法统宗》中有如下问题:"远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?"意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏 B.3盏 C.5盏 D.9盏
已知椭圆
的左焦点为
,右顶点为A,点E的坐标为(0,c),
的面积为
.
(I)求椭圆的离心率;
(II)设点Q在线段AE上, ,延长线段FQ与椭圆交于点P,点M,N在x轴上, ,且直线PM与直线QN间的距离为c,四边形PQNM的面积为3c.
(i)求直线FP的斜率;
(ii)求椭圆的方程.
设a,
,
.已知函数
,
.
(Ⅰ)求 的单调区间;
(Ⅱ)已知函数 和 的图象在公共点 处有相同的切线,
(i)求证: 处的导数等于0;
(ii)若关于x的不等式 在区间 上恒成立,求b的取值范围.
已知
为等差数列,前
项和为
,
是首项为2的等比数列,且公比大于0,
,
,
.
(Ⅰ)求 和 的通项公式;
(Ⅱ)求数列 的前n项和 .
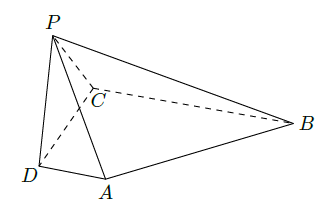
如图,在四棱锥
中,
平面
,
,
,
,
,
,
.
(I)求异面直线AP与BC所成角的余弦值;
(II)求证: ;
(II)求直线AB与平面PBC所成角的正弦值.
电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
| |
连续剧播放时长(分钟) |
广告播放时长(分钟) |
收视人次(万) |
| 甲 |
70 |
5 |
60 |
| 乙 |
60 |
5 |
25 |
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.
(I)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
在
中,内角A,B,C所对的边分别为a,b,c.已知
,
.
(Ⅰ)求 的值;
(Ⅱ)求 的值.