从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
执行如图的程序框图,如果输入的 a=﹣1,则输出的 S=( )
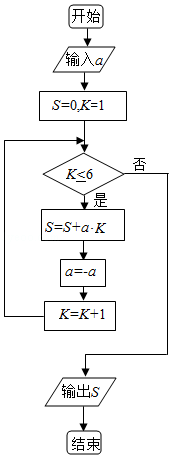
| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
| A. |
乙可以知道四人的成绩 |
| B. |
丁可以知道四人的成绩 |
| C. |
乙、丁可以知道对方的成绩 |
| D. |
乙、丁可以知道自己的成绩 |
函数 f( x)= ln( x 2﹣2 x﹣8)的单调递增区间是( )
| A. |
(﹣∞,﹣2) |
B. |
(﹣∞,﹣1) |
C. |
(1,+∞) |
D. |
(4,+∞) |
设 x, y满足约束条件 ,则 z=2 x+ y的最小值是( )
| A. |
﹣15 |
B. |
﹣9 |
C. |
1 |
D. |
9 |
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
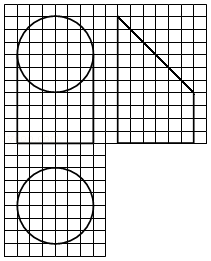
| A. |
90π |
B. |
63π |
C. |
42π |
D. |
36π |
若 a>1,则双曲线 y 2=1的离心率的取值范围是( )
| A. |
( ,+∞) |
B. |
( ,2) |
C. |
(1, ) |
D. |
(1,2) |
设非零向量 , 满足| |=| |则( )
| A. | ⊥ |
B. | | |=| | |
C. | ∥ |
D. | | |>| | |
函数 f( x)=sin(2 x )的最小正周期为( )
| A. |
4π |
B. |
2π |
C. |
π |
D. |
|
(1+ i)(2+ i)=( )
| A. |
1﹣i |
B. |
1+3i |
C. |
3+i |
D. |
3+3i |
设集合 A={1,2,3}, B={2,3,4},则 A∪ B=( )
| A. |
{1,2,3,4} |
B. |
{1,2,3} |
C. |
{2,3,4} |
D. |
{1,3,4} |
[选修4-5:不等式选讲]
已知函数 .
(1)当 时,求不等式 的解集;
(2)若不等式 的解集包含 ,求 a的取值范围.
[选修4―4:坐标系与参数方程]
在直角坐标系 中,曲线 C的参数方程为 ,直线 l的参数方程为 .
(1)若 ,求 C与 l的交点坐标;
(2)若 C上的点到 l的距离的最大值为 ,求a.
已知函数 .
(1)讨论 的单调性;
(2)若 有两个零点,求a的取值范围.