如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
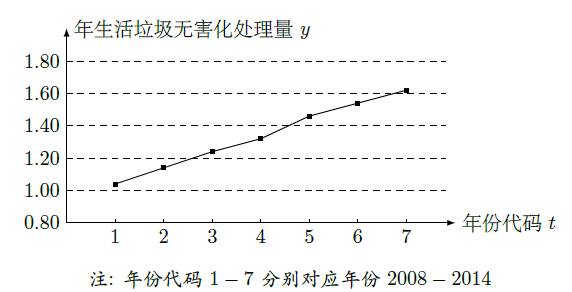
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: , , , .
参考公式: ,回归方程 中斜率和截距的最小二乘估计公式分别为:
, .
推荐套卷
如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.

(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: , , , .
参考公式: ,回归方程 中斜率和截距的最小二乘估计公式分别为:
, .