(本小题满分10分)设 且
且 ,集合
,集合 的所有
的所有 个元素的子集记为
个元素的子集记为 .
.
(1)求集合 中所有元素之和
中所有元素之和 ;
;
(2)记 为
为
 中最小元素与最大元素之和,求
中最小元素与最大元素之和,求 的值.
的值.
(本小题满分14分)已知函数 ,且对任意
,且对任意 ,都有
,都有 .
.
(1)求 ,
, 的关系式;
的关系式;
(2)若 存在两个极值点
存在两个极值点 ,
, ,且
,且 ,求出
,求出 的取值范围并证明
的取值范围并证明 ;
;
(3)在(2)的条件下,判断 零点的个数,并说明理由.
零点的个数,并说明理由.
(本小题满分14分)已知平面上的动点 与点
与点 连线的斜率为
连线的斜率为 ,线段
,线段 的中点与原点连线的斜率为
的中点与原点连线的斜率为 ,
, (
( ),动点
),动点 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)恰好存在唯一一个同时满足以下条件的圆:
①以曲线 的弦
的弦 为直径;
为直径;
②过点 ;
;
③直径 .求
.求 的取值范围.
的取值范围.
(本小题满分14分)在直角坐标系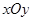 中,曲线
中,曲线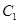 上的点均在圆
上的点均在圆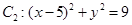 外,且对
外,且对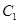 上任意一点
上任意一点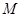 ,
,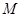 到直线
到直线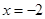 的距离等于该点与圆
的距离等于该点与圆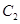 上点的距离的最小值.
上点的距离的最小值.
(1)求曲线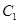 的方程;
的方程;
(2)设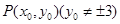 为圆
为圆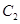 外一点,过
外一点,过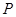 作圆
作圆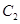 的两条切线,分别与曲线
的两条切线,分别与曲线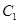 相交于点
相交于点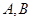 和
和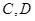 .证明:当
.证明:当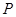 在直线
在直线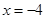 上运动时,四点
上运动时,四点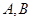
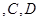 的纵坐标之积为定值.
的纵坐标之积为定值.
(本小题满分15分)已知 ,
, 是平面上的两个定点,动点
是平面上的两个定点,动点 满足
满足 .
.
(Ⅰ)求动点 的轨迹方程;
的轨迹方程;
(Ⅱ)已知圆方程为 ,过圆上任意一点作圆的切线,切线与(Ⅰ)中的轨迹交于
,过圆上任意一点作圆的切线,切线与(Ⅰ)中的轨迹交于 ,
, 两
两
点, 为坐标原点,设
为坐标原点,设 为
为 的中点,求
的中点,求 长度的取值范围.
长度的取值范围.
已知曲线 :
: ,将曲线
,将曲线 每一点的横坐标缩短为
每一点的横坐标缩短为 倍,纵坐标缩短为原来的
倍,纵坐标缩短为原来的 倍,得曲线
倍,得曲线 .以坐标原点
.以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程是
的极坐标方程是 .
.
(Ⅰ)写出曲线 的参数方程,直线
的参数方程,直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)过曲线 上任意一点
上任意一点 作与
作与 夹角为
夹角为 的直线,交
的直线,交 于点
于点 ,
, 的最大值与最小值.
的最大值与最小值.
(本小题满分14分)已知函数 ,
, (
( 为常数,
为常数, 是自然对数的底数),
是自然对数的底数), 为
为 的导函数,且
的导函数,且 .
.
(1)求 的值;
的值;
(2)对任意 ,证明:
,证明: ;
;
(3)若对所有的 ≥0,都有
≥0,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知椭圆
 (
( )的右焦点
)的右焦点 是抛物线
是抛物线 的焦点,过点
的焦点,过点 垂直于
垂直于 轴的直线被椭圆
轴的直线被椭圆 所截得的线段长度为
所截得的线段长度为 .
.
(1)求椭圆 的方程;
的方程;
(2)设动直线
 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 .请问:在
.请问:在 轴
轴
上是否存在定点 ,使得
,使得 为定值?若存在,求出点
为定值?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
一般地,我们把离心率为 的椭圆称为“黄金椭圆”.对于下列命题:
的椭圆称为“黄金椭圆”.对于下列命题:
①椭圆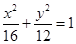 是黄金椭圆;
是黄金椭圆;
②若椭圆 是黄金椭圆,则
是黄金椭圆,则 ;
;
③在 中,
中,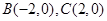 ,且点
,且点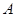 在以
在以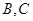 为焦点的黄金椭圆上,则
为焦点的黄金椭圆上,则 的周长为
的周长为 ;
;
④过黄金椭圆 的右焦点
的右焦点 作垂直于长轴的垂线,交椭圆于
作垂直于长轴的垂线,交椭圆于 两点,则
两点,则 ;
;
⑤设 是黄金椭圆
是黄金椭圆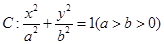 的两个焦点,则椭圆
的两个焦点,则椭圆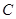 上满足
上满足 的点
的点 不
不
存在.
其中所有正确命题的序号是___________(把你认为正确命题的序号都填上).
(本小题满分13分)已知函数 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)设函数 ,且
,且 在定义域上为单调递增函数,求
在定义域上为单调递增函数,求 的取值范围;
的取值范围;
(3)若 ,在
,在 上存在一点
上存在一点 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
(本小题满分14分)如图,已知椭圆 :
: 的离心率为
的离心率为 ,
,  、
、 、
、 、
、 是其四个顶点,且四边形
是其四个顶点,且四边形 的面积为
的面积为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知直线 与椭圆
与椭圆 交于
交于 、
、 两点,
两点,
(ⅰ)若直线 过点
过点 ,则是否存在直线
,则是否存在直线 ,使得以
,使得以 为直径的圆经过点
为直径的圆经过点 ?求直线
?求直线 的方程;如果存在求出直线
的方程;如果存在求出直线 的方程;如果不存在,是说明理由.
的方程;如果不存在,是说明理由.
(ⅱ)若 ,且坐标原点在以
,且坐标原点在以 为直径的圆外,求该直线在
为直径的圆外,求该直线在 轴上的截距的取值范围.
轴上的截距的取值范围.