(本小题满分14分)如图,四棱锥 中,
中, ,底面
,底面 为梯形,
为梯形,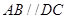 ,
, ,且
,且 ,
,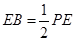 .
.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分14分)已知各项不为零的数列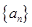 的前
的前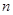 项和为
项和为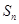 ,且满足
,且满足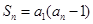 .
.
(1)求数列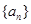 的通项公式;
的通项公式;
(2)设数列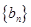 满足
满足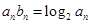 ,求数列
,求数列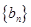 的前
的前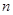 项和
项和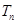 .
.
(本小题满分13分)如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
, .
.
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为 ,
, ,求证:
,求证: ;
;
(3)试问 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
【改编】(本小题满分13分)已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)当 时,
时, ,求实数
,求实数 的取值范围.
的取值范围.
【改编】(本小题满分13分)已知F1、F2分别为椭圆C: (a>b>0)的左、右焦点, 且离心率为
(a>b>0)的左、右焦点, 且离心率为 ,点
,点 在椭圆C上.
在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在斜率为k的直线 与椭圆C交于不同的两点M、N,使直线
与椭圆C交于不同的两点M、N,使直线 与
与 的倾斜角互补,且直线
的倾斜角互补,且直线 是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
【原创】(本小题满分12分)已知.
(Ⅰ)求函数的最小正周期和对称中心;
(Ⅱ)将函数的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,当时,方程
的图象,当时,方程 有实数解,求实数的取值范围.
有实数解,求实数的取值范围.
已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别为
的左、右焦点分别为 的左、右顶点,而
的左、右顶点,而 的左、右顶点分别是
的左、右顶点分别是 的左、右焦点。
的左、右焦点。
(1)求双曲线 的方程;
的方程;
(2)若直线 与椭圆
与椭圆 及双曲线
及双曲线 都恒有两个不同的交点,且L与的两个焦点A和B满足
都恒有两个不同的交点,且L与的两个焦点A和B满足 (其中O为原点),求
(其中O为原点),求 的取值范围。
的取值范围。
(本小题满分14分)若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(1)求 的极值;
的极值;
(2)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
某果园要将一批水果用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由果园承担.
若果园恰能在约定日期(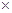 月
月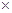 日)将水果送到,则销售商一次性支付给果园20万元; 若在约定日期前送到,每提前一天销售商将多支付给果园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给果园1万元.
日)将水果送到,则销售商一次性支付给果园20万元; 若在约定日期前送到,每提前一天销售商将多支付给果园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给果园1万元.
为保证水果新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送水果,已知下表内的信息:
| 统计信息 汽车行驶路线 |
不堵车的情况下到达城市乙所需 时间(天) |
堵车的情况下到达城市乙所需时间(天) |
堵车的概率 |
运费(万元) |
| 公路1 |
2 |
3 |
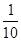 |
 |
| 公路2 |
1 |
4 |
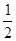 |
 |
(注:毛利润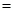 销售商支付给果园的费用
销售商支付给果园的费用 运费)
运费)
(1)记汽车走公路1时果园获得的毛利润为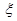 (单位:万元),求
(单位:万元),求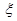 的分布列和数学期望
的分布列和数学期望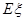 ;
;
(2)假设你是果园的决策者,你选择哪条公路运送水果有可能让果园获得的毛利润更多?
设椭圆 :
: 的左、右焦点分别是
的左、右焦点分别是 、
、 ,下顶点为
,下顶点为 ,线段
,线段 的中点为
的中点为 (
( 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线 :
: 与
与 轴的交点为
轴的交点为 ,且经过
,且经过 、
、 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 ,
, 为抛物线
为抛物线 上的一动点,过点
上的一动点,过点 作抛物线
作抛物线 的切线交椭圆
的切线交椭圆 于
于 、
、 两点,求
两点,求 面积的最大值.
面积的最大值.
对定义在区间D上的函数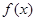 和
和 ,如果对任意
,如果对任意 ,都有
,都有 成立,那么称函数
成立,那么称函数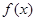 在区间D上可被
在区间D上可被 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①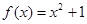 在区间
在区间 上可被
上可被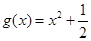 替代;
替代;
② 可被
可被 替代的一个“替代区间”为
替代的一个“替代区间”为 ;
;
③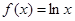 在区间
在区间 可被
可被 替代,则
替代,则 ;
;
④ ,则存在实数
,则存在实数 ,使得
,使得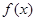 在区间
在区间 上被
上被 替代;
替代;
其中真命题的有
设函数 (
( ).
).
(1)当 时,求过点
时,求过点 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点 ,
, ,且
,且 ,记
,记 表示不大于
表示不大于 的最大整数,试比较
的最大整数,试比较 与
与 的大小.
的大小.
已知定点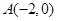 ,
, ,定直线
,定直线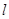 :
: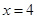 ,动点
,动点 与点
与点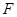 的距离是它到直线
的距离是它到直线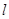 的距离的
的距离的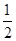 .设点
.设点 的轨迹为
的轨迹为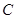 ,过点
,过点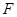 的直线交
的直线交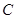 于
于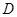 、
、 两点,直线
两点,直线 、
、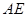 与直线
与直线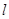 分别相交于
分别相交于 、
、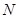 两点.
两点.
(1)求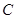 的方程;
的方程;
(2)以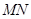 为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由.
为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由.
已知点 、
、 为双曲线
为双曲线 :
:
 的左、右焦点,过
的左、右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线 于点
于点 ,且
,且 ,圆
,圆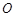 的方程是
的方程是 .
.
(1)求双曲线 的方程;
的方程;
(2)过双曲线 上任意一点
上任意一点 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、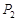 ,求
,求 的值;
的值;
(3)过圆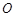 上任意一点
上任意一点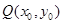 作圆
作圆 的切线
的切线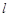 交双曲线
交双曲线 于
于 、
、 两点,
两点,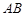 中点为
中点为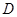 ,求证:
,求证: .
.