期中备考总动员高三理数学模拟卷【福建】4
【改编】若 ,则“
,则“ ”是“直线
”是“直线 和直线
和直线 互相垂直”的( )
互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
【改编】函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,只需把
的图象,只需把 的图象上所有点( )个单位长度.
的图象上所有点( )个单位长度.

A.向右平移 |
B.向右平移 |
C.向左平移 |
D.向左平移 |
如图,互不相同的点 ,
, , ,
, , , 和
, 和 ,
, , ,
, , , 分别在角O的两条边上,所有
, 分别在角O的两条边上,所有 相互平行,且所有梯形
相互平行,且所有梯形 的面积均相等.设
的面积均相等.设 ,若
,若 ,
, ,则
,则 =( )
=( )
A. |
B. |
C. |
D. |
我班制定了数学学习方案: 星期一和星期日分别解决4个数学问题, 且从星期二开始, 每天所解决问题的个数与前一天相比, 要么“多一个”要么“持平”要么“少一个”.在一周中每天所解决问题个数的不同方案共有( )
| A.50种 | B.51种 | C.140种 | D.141种 |
已知F是双曲线 的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为 ( )
的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为 ( )
A.(1,+∞) B.(1,2) C.(1,1+ ) D.(2,1+
) D.(2,1+ )
)
如图,己知 ,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,
,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点, ,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).
,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).

①x≥0,y≥0;②x-y≥0;③x-y≤0;④x-2y≥0;⑤2x-y≥0.
(本小题满分12分)已知 .
.
(Ⅰ)求 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(Ⅱ)在 中,角
中,角 所对应的边分别为
所对应的边分别为 ,若有
,若有 ,
, ,
, ,求
,求 的面积.
的面积.
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第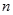 层第
层第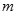 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为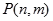 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第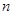 层的第
层的第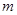 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.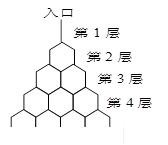
(Ⅰ)试求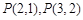 及
及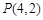 的值,并猜想
的值,并猜想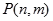 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第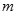 个竖直通道得到分数为
个竖直通道得到分数为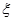 ,其中
,其中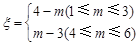 ,试求
,试求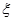 的分布列及数学期望.
的分布列及数学期望.
【改编】如图,在 中,
中, 为
为 边上的高,
边上的高, ,
, ,沿
,沿 将
将 翻折,使得
翻折,使得 ,得到几何体
,得到几何体 。
。
(1)求证: ;
;
(2)求 与平面
与平面 所成角的正切值;
所成角的正切值;
(3)求二面角 的余弦值.
的余弦值.
已知点 、
、 为双曲线
为双曲线 :
:
 的左、右焦点,过
的左、右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线 于点
于点 ,且
,且 ,圆
,圆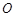 的方程是
的方程是 .
.
(1)求双曲线 的方程;
的方程;
(2)过双曲线 上任意一点
上任意一点 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、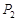 ,求
,求 的值;
的值;
(3)过圆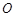 上任意一点
上任意一点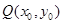 作圆
作圆 的切线
的切线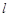 交双曲线
交双曲线 于
于 、
、 两点,
两点,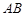 中点为
中点为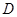 ,求证:
,求证: .
.
(本小题满分7分)选修4—2:矩阵与变换
已知直线 在矩阵
在矩阵 对应的变换作用下变为直线
对应的变换作用下变为直线 .
.
(Ⅰ)求实数 ,
, 的值;
的值;
(Ⅱ)若点 在直线
在直线 上,且
上,且 ,求点
,求点 的坐标.
的坐标.
(本小题满分7分)《选修4-4:坐标系与参数方程》
在直角坐标系中,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ,曲线D的参数方程为
,曲线D的参数方程为 (
( 为参数).
为参数).
(Ⅰ)把C的极坐标方程化为直角坐标方程;
(Ⅱ)判定曲线C与曲线D间的位置关系.
 ,
, 为虚数单位,
为虚数单位, ,若
,若 ,则复数
,则复数 的共轭复数
的共轭复数 的虚部是( )
的虚部是( )



 ,则这四个数的大小关系是( )
,则这四个数的大小关系是( )



 的图象大致为( )
的图象大致为( )
 、
、 满足
满足 ,且
,且 的最大值等于
的最大值等于 ,则正实数
,则正实数 的值等于( )
的值等于( )



 与曲线
与曲线 有四个不同交点,则实数
有四个不同交点,则实数 的取值范围是 ( ).
的取值范围是 ( ).




 的
的 的边
的边 上任取一点P,则△PBC的面积不小于
上任取一点P,则△PBC的面积不小于 的概率是 .
的概率是 . 的最大值是______________
的最大值是______________ 中,底面
中,底面 是平行四边形,点
是平行四边形,点 为
为 的中点,则面
的中点,则面 将四棱锥
将四棱锥 所分成的上下两部分的体积的比值为 .
所分成的上下两部分的体积的比值为 .

 的单调性.
的单调性. (
( ,e为自然对数的底数)
,e为自然对数的底数) 满足
满足 ,
, ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号