期中备考总动员高三理数学模拟卷【福建】5
【原创】在锐角 中 “
中 “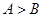 ”是“
”是“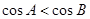 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
如图,平行四边形 中,
中, ,
, 是线段
是线段 上,且满足
上,且满足 ,若
,若 为平行四边形
为平行四边形 内任意一点(含边界),则
内任意一点(含边界),则 的最大值为( )
的最大值为( )
| A.13 | B.0 | C.8 | D.5 |
已知双曲线
 的离心率为4,过右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于点H,若
的离心率为4,过右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于点H,若 ,则
,则 =( )
=( )
| A.14 | B.16 | C.18 | D.20 |
某学校周五安排有语文、数学、英语、物理、化学、体育六节课,要求体育不排在第一节课,数学不排在第四节课,则这天课表的不同排法种数为( )
| A.600 | B.288 | C.480 | D.504 |
某天,甲要去银行办理储蓄业务,已知银行的营业时间为9: 00至17:00,设甲在当天13:00至18:00之间任何时间去银行的可能性相同,那么甲去银行恰好能办理业务的概率是 .
对于四面体ABCD,以下命题中,真命题的序号为 (填上所有真命题的序号)
①若 为
为 中点,则平面
中点,则平面 平面
平面 ;
;
②若 ,则
,则 ;
;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为 ;
;
④若以A为端点的三条棱所在直线两两垂直,则 在平面
在平面 内的射影为
内的射影为 的垂心;
的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
在如图所示的几何体中,四边形 是等腰梯形,
是等腰梯形, ∥
∥ ,
, ,
, .在梯形
.在梯形 中,
中, ∥
∥ ,且
,且 ,
, ⊥平面
⊥平面 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若二面角 为
为 ,求
,求 的长.
的长.
由于我市去年冬天多次出现重度污染天气,市政府决定从今年3月份开始进行汽车尾气的整治,为降低汽车尾气的排放量,我市某厂生产了甲、乙两种不同型号的节排器,分别从两种节排器中随机抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.

节排器等级如表格所示
| 综合得分K的范围 |
节排器等级 |
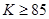 |
一级品 |
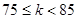 |
二级品 |
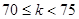 |
三级品 |
若把频率分布直方图中的频率视为概率,则
(1)如果从甲型号中按节排器等级用分层抽样的方法抽取10件,然后从这10件中随机抽取3件,求至少有2件一级品的概率;
(2)如果从乙型号的节排器中随机抽取3件,求其二级品数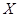 的分布列及数学期望.
的分布列及数学期望.
已知定点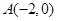 ,
, ,定直线
,定直线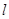 :
: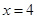 ,动点
,动点 与点
与点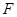 的距离是它到直线
的距离是它到直线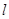 的距离的
的距离的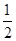 .设点
.设点 的轨迹为
的轨迹为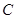 ,过点
,过点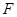 的直线交
的直线交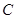 于
于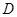 、
、 两点,直线
两点,直线 、
、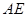 与直线
与直线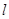 分别相交于
分别相交于 、
、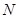 两点.
两点.
(1)求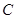 的方程;
的方程;
(2)以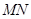 为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由.
为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由.
设函数 (
( ).
).
(1)当 时,求过点
时,求过点 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点 ,
, ,且
,且 ,记
,记 表示不大于
表示不大于 的最大整数,试比较
的最大整数,试比较 与
与 的大小.
的大小.
(本小题满分7分)选修4—2:矩阵与变换
已知二阶矩阵 有特征值λ1=4及属于特征值4的一个特征向量
有特征值λ1=4及属于特征值4的一个特征向量 并有特征值
并有特征值 及属于特征值-1的一个特征向量
及属于特征值-1的一个特征向量 ,
, 
(Ⅰ)求矩阵 ;(Ⅱ)求
;(Ⅱ)求 .
.
【改编】(本小题满分7分)选修4-4:极坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 ,(
,( 为参数),以原点
为参数),以原点 为极点,
为极点, 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求曲线 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设 为曲线
为曲线 上的动点,求点
上的动点,求点 到
到 上点的距离的最小值.
上点的距离的最小值.
 ,
, ,则
,则 ( )
( )



 的图象大致为( )
的图象大致为( )





 的夹角为
的夹角为 ,且
,且 ,在
,在 中,
中, ,D为BC的中点,则
,D为BC的中点,则 ( )
( )
 ,则
,则 =
= 中,
中, ,则
,则 与平面
与平面 所成角的正弦值等于( )
所成角的正弦值等于( )



 与曲线
与曲线 和
和 的交点分别为
的交点分别为 ,则线段
,则线段 的最小值为________.
的最小值为________. 的展开式中常数项为 .(用数字表示)
的展开式中常数项为 .(用数字表示) ,则
,则 的值是 .
的值是 .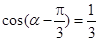 ,则
,则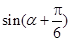 的值是 .
的值是 . ,其中A、B、C是
,其中A、B、C是 的三个内角,且满足
的三个内角,且满足 ,
, .
. 的值;
的值; ,且
,且 ,求
,求 的值.
的值. 为实数,且
为实数,且

 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号