对于四面体ABCD,以下命题中,真命题的序号为 (填上所有真命题的序号)
①若 为
为 中点,则平面
中点,则平面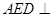 平面
平面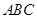 ;
;
②若 ,则
,则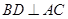 ;
;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为 ;
;
④若以A为端点的三条棱所在直线两两垂直,则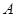 在平面
在平面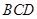 内的射影为
内的射影为 的垂心;
的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
推荐套卷
对于四面体ABCD,以下命题中,真命题的序号为 (填上所有真命题的序号)
①若 为
为 中点,则平面
中点,则平面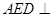 平面
平面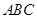 ;
;
②若 ,则
,则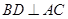 ;
;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为 ;
;
④若以A为端点的三条棱所在直线两两垂直,则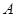 在平面
在平面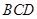 内的射影为
内的射影为 的垂心;
的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。