(本小题满分12分) 若数列 是等比数列,
是等比数列, ,公比
,公比 ,已知
,已知 和
和 的等差中项为
的等差中项为 ,且
,且 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和.
项和.
(本小题满分14分)已知椭圆 ,其中
,其中 为左、右焦点,O为坐标原点.直线l与椭圆交于
为左、右焦点,O为坐标原点.直线l与椭圆交于 两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
两个不同点.当直线l过椭圆C右焦点F2且倾斜角为 时,原点O到直线l的距离为
时,原点O到直线l的距离为 .又椭圆上的点到焦点F2的最近距离为
.又椭圆上的点到焦点F2的最近距离为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)以OP,OQ为邻边做平行四边形OQNP,当平行四边形OQNP面积为 时,求平行四边形OQNP的对角线之积
时,求平行四边形OQNP的对角线之积 的最大值;
的最大值;
(Ⅲ)若抛物线 为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
在平面直角坐标系 中,已知过点
中,已知过点 的椭圆
的椭圆 :
: 的右焦点为
的右焦点为 ,过焦点
,过焦点 且与
且与 轴不重合的直线与椭圆
轴不重合的直线与椭圆 交于
交于 ,
, 两点,点
两点,点 关于坐标原点的对称点为
关于坐标原点的对称点为 ,直线
,直线 ,
, 分别交椭圆
分别交椭圆 的右准线
的右准线 于
于 ,
, 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若点 的坐标为
的坐标为 ,试求直线
,试求直线 的方程;
的方程;
(3)记 ,
, 两点的纵坐标分别为
两点的纵坐标分别为 ,
, ,试问
,试问 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
(本小题满分16分)已知数列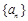 (
(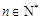 ,
,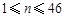 )满足
)满足 ,
,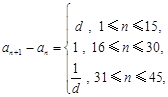 其中
其中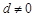 ,
,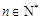 .
.
(1)当 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .
.
①若 ,
,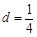 ,求证:
,求证: ;
;
②是否存在实数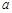 ,
, ,使
,使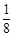 ,
,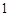 ,
,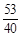 都属于
都属于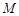 ?若存在,请求出实数
?若存在,请求出实数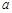 ,
, ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分15分)某飞机失联,经卫星侦查,其最后出现在小岛 附近.现派出四艘搜救船
附近.现派出四艘搜救船 ,为方便联络,船
,为方便联络,船 始终在以小岛
始终在以小岛 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛 到
到 的距离为
的距离为 ,
, 船到小岛
船到小岛 的距离为
的距离为 .
.
(1)请分别求 关于
关于 的函数关系式
的函数关系式 ;并分别写出定义域;
;并分别写出定义域;
(2)当 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即 最大).
最大).
【原创】(本小题满分14分)设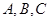 是单位圆上三点,
是单位圆上三点,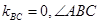 为锐角.
为锐角.
(1)若 求
求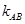
(2)若 求三角形
求三角形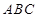 面积的最大值.
面积的最大值.
【原创】在平面直角坐标系 中,椭圆
中,椭圆 的左顶点为
的左顶点为 左焦点为
左焦点为 右焦点为
右焦点为 .
.
(1)若椭圆上存在点 ,使得
,使得 ,求椭圆
,求椭圆 离心率的取值范围;
离心率的取值范围;
(2)若点 满足
满足 ,求证:以
,求证:以 为圆心,以
为圆心,以 为半径的圆与椭圆
为半径的圆与椭圆 右准线相切.
右准线相切.
(本小题满分10分)在平面直角坐标系xOy中,已知抛物  的准线方程为
的准线方程为  过点M(0,-2)作抛物线的切线MA,切点为A(异于点O).直线
过点M(0,-2)作抛物线的切线MA,切点为A(异于点O).直线 过点M与抛物线交于两点B,C,与直线OA交于点N.
过点M与抛物线交于两点B,C,与直线OA交于点N.
(1)求抛物线的方程;
(2)试问:  的值是否为定值?若是,求出定值;若不是,说明理由。
的值是否为定值?若是,求出定值;若不是,说明理由。
(本小题满分14分)已知函数 ,其中
,其中 ,
, .
.
(1)当 ,
, 时,求函数
时,求函数 的最小值;
的最小值;
(2)当 ,且
,且 为常数时,若函数
为常数时,若函数 对任意的
对任意的 ,总有
,总有 成立,试用
成立,试用 表示出
表示出 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆
 (
( )的离心率为
)的离心率为 ,右焦点
,右焦点 到直线
到直线
 的距离为
的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过椭圆右焦点 ,斜率为
,斜率为 (
( )的直线
)的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 为椭圆的右顶点,
为椭圆的右顶点,
直线 ,
, 分别交直线
分别交直线 于点
于点 ,
, ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值.
(本小题满分14分)已知椭圆
 (
( )的右焦点
)的右焦点 ,点
,点
在椭圆 上.
上.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线 过点
过点 ,且与椭圆
,且与椭圆 交于
交于 ,
, 两点,过原点
两点,过原点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,如果
,如果 的
的
面积为 (
( 为实数),求
为实数),求 的值.
的值.
(本小题满分14分)已知椭圆 的中心在原点
的中心在原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,右焦点到右
,右焦点到右
顶点的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)是否存在与椭圆 交于
交于 ,
, 两点的直线
两点的直线
 (
( ),使得
),使得
成立?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分14分)已知椭圆 过点
过点 ,且长轴长等于4.
,且长轴长等于4.
(1)求椭圆C的方程;
(2) 是椭圆C的两个焦点,圆O是以
是椭圆C的两个焦点,圆O是以 为直径的圆,直线
为直径的圆,直线 与圆O相切,并与椭圆C交于不同的两点A,B,若
与圆O相切,并与椭圆C交于不同的两点A,B,若 ,求
,求 的值.
的值.
(本小题满分14分)已知函数 ,
, .
.
(Ⅰ) 时,证明:
时,证明: ;
;
(Ⅱ) ,若
,若 ,求a的取值范围.
,求a的取值范围.