期中备考总动员高三数学模拟卷【江苏】5
设向量 ,
, ,则“
,则“ ”是“
”是“ ”成立的 条件 (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) .
”成立的 条件 (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) .
设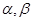 为互不重合的平面,
为互不重合的平面, 是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题:
①若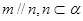 ,则
,则 ;
;
②若 ,则
,则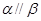 ;
;
③若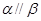 ,
,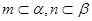 ,则
,则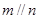 ;
;
④若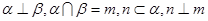 ,则
,则 ;
;
其中正确命题的序号为 .
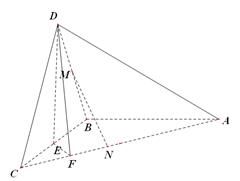
(本小题满分14分)如图,在三棱锥 中,已知
中,已知 是正三角形,
是正三角形,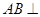 平面
平面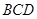 ,
, ,
,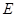 为
为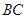 的中点,
的中点,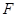 在棱
在棱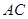 上,且
上,且 .
.
(1)求三棱锥 的体积;
的体积;
(2)求证: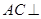 平面
平面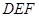 ;
;
(3)若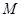 为
为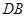 中点,
中点,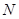 在棱
在棱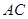 上,且
上,且 ,求证:
,求证: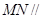 平面
平面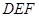 .
.
如图,某商业中心O有通往正东方向和北偏东30º方向的两条街道,某公园P位于商业中心北偏东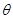 角(
角( ),且与商业中心O的距离为
),且与商业中心O的距离为 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
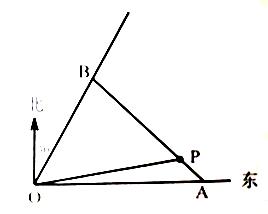
(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
【原创】在平面直角坐标系 中,椭圆
中,椭圆 的左顶点为
的左顶点为 左焦点为
左焦点为 右焦点为
右焦点为 .
.
(1)若椭圆上存在点 ,使得
,使得 ,求椭圆
,求椭圆 离心率的取值范围;
离心率的取值范围;
(2)若点 满足
满足 ,求证:以
,求证:以 为圆心,以
为圆心,以 为半径的圆与椭圆
为半径的圆与椭圆 右准线相切.
右准线相切.
(本小题满分16分)已知函数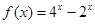 ,实数
,实数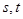 满足
满足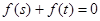 ,设
,设 .
.
(1)当函数 的定义域为
的定义域为 时,求
时,求 的值域;
的值域;
(2)求函数关系式 ,并求函数
,并求函数 的定义域;
的定义域;
(3)求 的取值范围.
的取值范围.
设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前 项和为
项和为 ,若
,若 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数 (
( ),求证:“
),求证:“ 且
且 ”是“
”是“ 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有
 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求 的取值范围.
的取值范围.
【原创】选修4-1:几何证明选讲(本小题满分10分)
如图, ,
, 是圆
是圆 的两条弦,它们相交于
的两条弦,它们相交于 的中点
的中点 ,若
,若 ,
, ,
, ,求圆
,求圆 的半径.
的半径.
【原创】选修4—4:坐标系与参数方程
在直角坐标系中,参数方程为 的直线
的直线 ,与以原点为极点,
,与以原点为极点, 轴的正半轴为极轴,极坐标方程为
轴的正半轴为极轴,极坐标方程为 的曲线
的曲线 相交于弦
相交于弦 ,若点
,若点 ,求
,求 的值.
的值.
(本小题满分10分)某校开设8门校本课程,其中4门课程为人文科学,4门为自然科学,学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(1)求某同学至少选修1门自然科学课程的概率;
(2)已知某同学所选修的3门课程中有1门人文科学,2门自然科学,若该同学通过人文科学课程的概率都是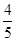 ,自然科学课程的概率都是
,自然科学课程的概率都是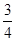 ,且各门课程通过与否相互独立.用
,且各门课程通过与否相互独立.用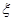 表示该同学所选的3门课程通过的门数,求随机变量
表示该同学所选的3门课程通过的门数,求随机变量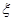 的概率分布列和数学期望。
的概率分布列和数学期望。
 满足
满足 为虚数单位
为虚数单位 ,则
,则 ,
, ,则
,则 .
. 次射箭的环数依次是
次射箭的环数依次是 ,则该组数据的方差是 .
,则该组数据的方差是 . ,则输出
,则输出 的值为 ..
的值为 ..

 中,以直线
中,以直线 为渐近线,且经过抛物线
为渐近线,且经过抛物线 焦点的双曲线的方程是 .
焦点的双曲线的方程是 . 对于任意
对于任意 若对于任意正整数
若对于任意正整数 ,在数列中恰有
,在数列中恰有 .
. 是奇函数,则
是奇函数,则 .
. ,
, 为
为 的一个极值点,且满足
的一个极值点,且满足 ,则
,则
 满足
满足 ,则
,则 的最大值为
的最大值为  满足
满足 ,则函数
,则函数 的图象所有交点的横坐标之和等于 .
的图象所有交点的横坐标之和等于 . 的前
的前 项和为
项和为 ,且
,且 且
且 ,则满足条件的所有正整数
,则满足条件的所有正整数 的值为 .
的值为 .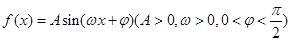 部分图象如图所示。
部分图象如图所示。
 的解析式;
的解析式;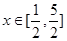 时,求函数
时,求函数 的值域。
的值域。 ,
, ,若矩阵
,若矩阵 对应的变换把直线
对应的变换把直线 变为直线
变为直线 ,求直线
,求直线 ,证明:
,证明: .
. ,
, 是
是 的两个非空子集,且满足集合
的两个非空子集,且满足集合 中的最大数小于集合
中的最大数小于集合 中的最小数,记满足条件的集合对
中的最小数,记满足条件的集合对 的个数为
的个数为 .
. 的值;
的值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号