(本小题满分10分)某校开设8门校本课程,其中4门课程为人文科学,4门为自然科学,学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(1)求某同学至少选修1门自然科学课程的概率;
(2)已知某同学所选修的3门课程中有1门人文科学,2门自然科学,若该同学通过人文科学课程的概率都是 ,自然科学课程的概率都是
,自然科学课程的概率都是 ,且各门课程通过与否相互独立.用
,且各门课程通过与否相互独立.用 表示该同学所选的3门课程通过的门数,求随机变量
表示该同学所选的3门课程通过的门数,求随机变量 的概率分布列和数学期望。
的概率分布列和数学期望。
相关知识点
推荐套卷
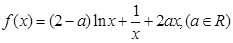
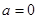 时,求
时,求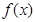 的极值;
的极值;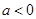 时,求
时,求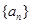 的前n项和为
的前n项和为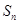 ,且
,且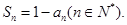
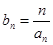 ,试求数列
,试求数列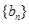 的前
的前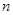 项和.
项和.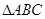 的三个内角
的三个内角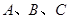 的对边分别为
的对边分别为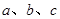 ,已知
,已知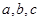 成等比数列,且
成等比数列,且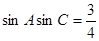

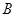 的大小;
的大小; 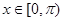 ,求函数
,求函数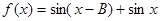 的值域.
的值域.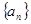 的首项
的首项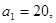 前
前 项和记为
项和记为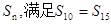 ,求
,求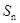 取得最大值,并求出最大值.
取得最大值,并求出最大值.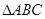 中,角
中,角 为锐角,记角
为锐角,记角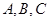 所对的边分别为
所对的边分别为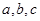 ,设向量
,设向量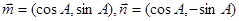 ,且
,且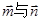 的夹角为
的夹角为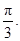
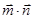 的值及角
的值及角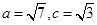 ,求
,求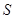 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号