设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前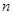 项和为
项和为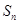 ,若
,若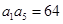 ,
,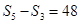 .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数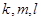 (
(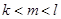 ),求证:“
),求证:“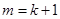 且
且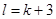 ”是“
”是“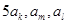 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列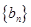 满足:对任意的正整数
满足:对任意的正整数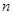 ,都有
,都有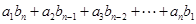
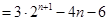 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求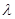 的取值范围.
的取值范围.
推荐套卷
设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前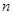 项和为
项和为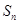 ,若
,若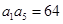 ,
,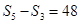 .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数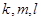 (
(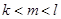 ),求证:“
),求证:“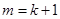 且
且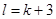 ”是“
”是“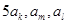 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列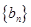 满足:对任意的正整数
满足:对任意的正整数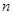 ,都有
,都有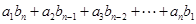
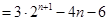 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求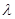 的取值范围.
的取值范围.