（本小题满分15分）已知椭圆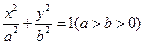
的离心率为
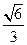，过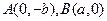
的直线与原点的距离为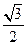
（1）求椭圆的方程；
（2）已知定点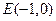
，直线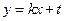
与椭圆交于不同两点C，D，试问：对任意的
，是否都存在实数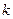
，使得以线段CD为直径的圆过点E？证明你的结论
相关试题
。
时，求该函数的值域；
对于
恒成立，求
的取值范围.
满足条件
和
.
上的最大值和最小值．
的终边过点P
，
的值
的符号推荐套卷
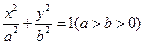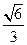（本小题满分15分）已知椭圆的离心率为，过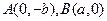的直线与原点的距离为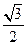
（1）求椭圆的方程；
（2）已知定点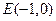，直线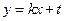与椭圆交于不同两点C，D，试问：对任意的，是否都存在实数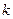，使得以线段CD为直径的圆过点E？证明你的结论
粤公网安备 44130202000953号