(本小题满分15分)
已知函数 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: 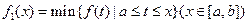 ,
,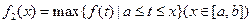
其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 在
在 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得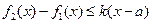 对任意的
对任意的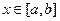 成立,则称函数
成立,则称函数 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(1)若 ,
, ,试写出
,试写出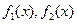 的表达式;
的表达式;
(2)已知函数 ,
,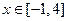 ,试判断
,试判断 是否为
是否为 上的“
上的“ 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知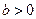 ,函数
,函数 是
是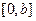 上的2阶收缩函数,求
上的2阶收缩函数,求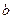 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分15分)
已知函数 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: 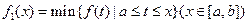 ,
,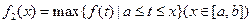
其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 在
在 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得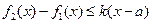 对任意的
对任意的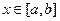 成立,则称函数
成立,则称函数 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(1)若 ,
, ,试写出
,试写出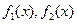 的表达式;
的表达式;
(2)已知函数 ,
,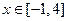 ,试判断
,试判断 是否为
是否为 上的“
上的“ 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知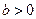 ,函数
,函数 是
是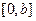 上的2阶收缩函数,求
上的2阶收缩函数,求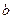 的取值范围.
的取值范围.