本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
已知数列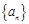 是首项为3,公比为
是首项为3,公比为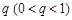 的无穷等比数列,且数列
的无穷等比数列,且数列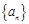 各项的和等于9.对给定的
各项的和等于9.对给定的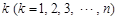 ,设
,设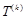 是首项为
是首项为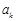 ,公差为
,公差为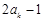 的等差数列.
的等差数列.
(1)求数列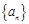 的通项
的通项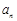 ;
;
(2)求数列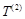 的前10项之和;
的前10项之和;
(3)设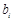 为数列
为数列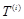 的第
的第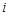 项,
项,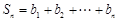 ,求
,求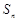 ,并求正整数
,并求正整数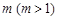 ,使得
,使得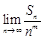 存在且不等于零.
存在且不等于零.
已知椭圆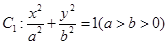 与圆
与圆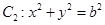 ,若在椭圆
,若在椭圆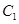 上存在点P,过P作圆的切线PA,PB,切点为A,.B使得
上存在点P,过P作圆的切线PA,PB,切点为A,.B使得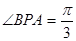 ,则椭圆
,则椭圆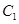 的离心率的取值范围是( )
的离心率的取值范围是( )
A.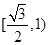 |
B.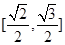 |
C.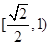 |
D.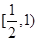 |
(小题满分12)椭圆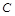 的方程为
的方程为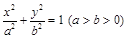 ,
,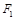 、
、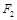 分别是它的左、右焦点,已知椭圆
分别是它的左、右焦点,已知椭圆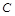 过点
过点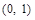 ,且离心率
,且离心率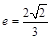 .
.
(1)求椭圆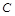 的方程;
的方程;
(2)如图,设椭圆的左、右顶点分别为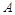 、
、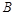 ,直线
,直线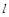 的方程为
的方程为 ,
,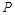 是椭圆上异于
是椭圆上异于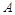 、
、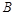 的任意一点,直线
的任意一点,直线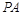 、
、 分别交直线
分别交直线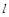 于
于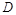 、
、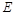 两点,求
两点,求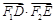 的值;
的值;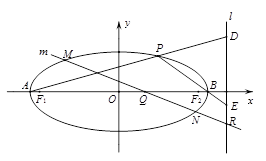
(3)过点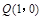 任意作直线
任意作直线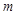 (与
(与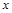 轴不垂直)与椭圆
轴不垂直)与椭圆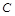 交于
交于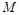 、
、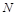 两点,与
两点,与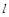 交于
交于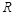 点,
点,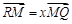 ,
, . 求证:
. 求证: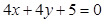 .
.
(本小题满分12分)已知公比为负值的等比数列 中,
中, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一
人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了 份,统计结果如下面的图表所示.
份,统计结果如下面的图表所示.
| 组号 |
年龄 分组 |
答对全卷 的人数 |
答对全卷的人数 占本组的概率 |
| 1 |
[20,30) |
28 |
 |
| 2 |
[30,40) |
27 |
0.9 |
| 3 |
[40,50) |
5 |
0.5 |
| 4 |
[50,60] |
 |
0.4 |
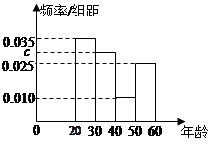
(1)分别求出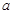 ,
, ,
,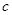 ,
, 的值;
的值;
(2)从第3,4组答对全卷的人中用分层抽样的方法抽取6人,在所抽取的6人中随机抽取2人授予“环
保之星”,记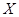 为第3组被授予“环保之星”的人数,求
为第3组被授予“环保之星”的人数,求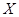 的分布列与数学期望.
的分布列与数学期望.
(本小题满分13分)已知椭圆 :
:
 的焦距为
的焦距为 ,其短轴的两个端点与长轴的一个端点构成正三角形.
,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆 的标准方程;
的标准方程;
(2)设 为椭圆
为椭圆 的左焦点,
的左焦点, 为直线
为直线 上任意一点,过
上任意一点,过 作
作 的垂线交椭圆
的垂线交椭圆 于点
于点 ,
, ,
,
①证明: 平分线段
平分线段 (其中
(其中 为坐标原点),
为坐标原点),
②当 值最小时,求点
值最小时,求点 的坐标.
的坐标.
(本小题满分13分)某批产品成箱包装,每箱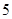 件.一用户在购进该批产品前先取出
件.一用户在购进该批产品前先取出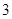 箱,设取出的
箱,设取出的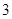 箱中,第一,二,三箱中分别有
箱中,第一,二,三箱中分别有 件,
件,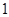 件,
件, 件二等品,其余为一等品.
件二等品,其余为一等品.
(1)在取出的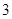 箱中,若该用户从第三箱中有放回的抽取
箱中,若该用户从第三箱中有放回的抽取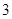 次(每次一件),求恰有两次抽到二等品的概率;
次(每次一件),求恰有两次抽到二等品的概率;
(2)在取出的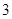 箱中,若该用户再从每箱中任意抽取
箱中,若该用户再从每箱中任意抽取 件产品进行检验,用
件产品进行检验,用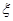 表示抽检的
表示抽检的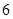 件产品中二等品的件数,求
件产品中二等品的件数,求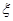 的分布列及数学期望.
的分布列及数学期望.
(本小题满分13分)已知函数


 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函
,纵坐标不变,得到函
数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值.
上的最小值.
本题共有2个小题,第1小题满分5分,第2小题满分9分.
某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数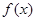 与时刻
与时刻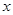 (时)的关系为
(时)的关系为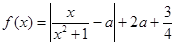 ,
,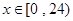 ,其中
,其中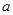 是与气象有关的参数,且
是与气象有关的参数,且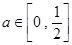 .若用每天
.若用每天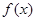 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作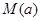 .
.
(1)令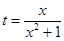 ,
,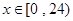 ,求
,求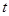 的取值范围;
的取值范围;
(2)求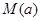 的表达式,并规定当
的表达式,并规定当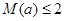 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当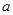 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
已知方程 在
在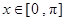 上有两个不相等的实数解,则实数
上有两个不相等的实数解,则实数 的取值范围是____________.
的取值范围是____________.
本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油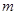 万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前
万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前 个月的需求量
个月的需求量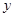 (万吨)与
(万吨)与 的函数关系为
的函数关系为 ,并且前4个月,区域外的需求量为20万吨.
,并且前4个月,区域外的需求量为20万吨.
(1)试写出第 个月石油调出后,油库内储油量
个月石油调出后,油库内储油量 (万吨)与
(万吨)与 的函数关系式;
的函数关系式;
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定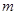 的取值范围.
的取值范围.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,它的一个顶点恰好经过抛物线
轴上,它的一个顶点恰好经过抛物线 的准线,且经过点
的准线,且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2) 若直线
若直线 的方程为
的方程为 .
. 是经过椭圆左焦点
是经过椭圆左焦点 的任一弦,设直线
的任一弦,设直线 与直线
与直线 相交于点
相交于点 ,记
,记 的斜率分别为
的斜率分别为 .试探索
.试探索 之间有怎样的关系式?给出证明过程.
之间有怎样的关系式?给出证明过程.
(本小题满分16分)已知函数 ,
, ,设
,设 .
.
(1)若 在
在 处取得极值,且
处取得极值,且 ,求函数h(x)的单调区间;
,求函数h(x)的单调区间;
(2)若 时函数h(x)有两个不同的零点x1,x2.
时函数h(x)有两个不同的零点x1,x2.
①求b的取值范围;②求证: .
.