江西省鹰潭市高三第一次模拟考试理科数学试卷
已知 为虚数单位,
为虚数单位, 为实数,复数
为实数,复数 在复平面内对应的点为
在复平面内对应的点为 ,则“
,则“ ”是“点
”是“点 在第四象限”的( )
在第四象限”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条 |
已知命题 :函数
:函数 的最小正周期为
的最小正周期为 ;命题
;命题 :若函数
:若函数 为偶函数,则
为偶函数,则 关于
关于 对称.则下列命题是真命题的是( )
对称.则下列命题是真命题的是( )
A. |
B. |
C. |
D. |
甲乙两人从 门课程中各选修两门,则甲乙所选的课程中至少有
门课程中各选修两门,则甲乙所选的课程中至少有 门不相同的选法共有( )
门不相同的选法共有( )
| A.30种 | B.36种 | C.60种 | D.72种 |
已知 是双曲线
是双曲线 的左焦点,过
的左焦点,过 作倾斜角为
作倾斜角为 的直线
的直线 ,直线
,直线 与双曲线交于点
与双曲线交于点 与
与 轴交于点
轴交于点 且
且 ,则该双曲线的离心率等于( )
,则该双曲线的离心率等于( )
A. |
B. |
C. |
D. |
(本小题满分12分)已知公比为负值的等比数列 中,
中, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)湖南卫视“我是歌手”这个节目深受广大观众喜爱,节目每周直播一次,在某周比赛中歌手甲、乙、丙竞演完毕,现场的某 位大众评审对这
位大众评审对这 位歌手进行投票,每位大众评审只能投一票且把票投给任一歌手是等可能的,求:
位歌手进行投票,每位大众评审只能投一票且把票投给任一歌手是等可能的,求:
(1)恰有 人把票投给歌手甲的概率;
人把票投给歌手甲的概率;
(2)投票结束后得票歌手的个数 的分布列与期望.
的分布列与期望.
(本小题满分12分)在如图所示的几何体中, 平面
平面 ,
, ∥
∥ ,
, 是
是 的中点,
的中点,
 ,
, ,
, .
.
(1)证明 平面
平面 ;
;
(2)求二面角 的余弦值的大小.
的余弦值的大小.
(小题满分12)椭圆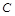 的方程为
的方程为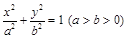 ,
,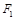 、
、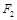 分别是它的左、右焦点,已知椭圆
分别是它的左、右焦点,已知椭圆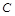 过点
过点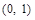 ,且离心率
,且离心率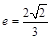 .
.
(1)求椭圆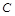 的方程;
的方程;
(2)如图,设椭圆的左、右顶点分别为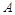 、
、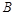 ,直线
,直线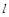 的方程为
的方程为 ,
,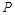 是椭圆上异于
是椭圆上异于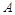 、
、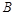 的任意一点,直线
的任意一点,直线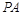 、
、 分别交直线
分别交直线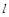 于
于 、
、 两点,求
两点,求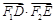 的值;
的值;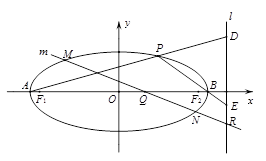
(3)过点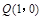 任意作直线
任意作直线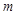 (与
(与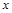 轴不垂直)与椭圆
轴不垂直)与椭圆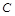 交于
交于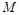 、
、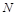 两点,与
两点,与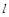 交于
交于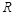 点,
点,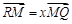 ,
, . 求证:
. 求证: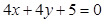 .
.
(本大题满分12分)已知函数 ,
, ,
, 图象与
图象与 轴异于原点的交点
轴异于原点的交点 处的切线为
处的切线为 ,
, 与
与 轴的交点N处的切线为
轴的交点N处的切线为 , 并且
, 并且 与
与 平行.
平行.
(1)求 的值;
的值;
(2)已知实数 ,求
,求 的取值范围及函数
的取值范围及函数 的最小值;
的最小值;
(3)令 ,给定
,给定 ,对于两个大于
,对于两个大于 的正数
的正数 ,存在实数
,存在实数 满足:
满足: ,
, ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数 的取值范围..
的取值范围..
(本小题满分10分)选修4—1:几何证明选讲
如图, 内接于直径为
内接于直径为 的圆
的圆 ,过点
,过点 作圆
作圆 的切线交
的切线交 的延长线于点
的延长线于点 ,
, 的平分线分别交
的平分线分别交 和圆
和圆 于点
于点 ,若
,若 .
.
(1)求证: ;
;
(2)求 的值.
的值.
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 是参数
是参数 .
.
(1)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线 与曲线
与曲线 相交于
相交于 、
、 两点,且
两点,且 ,求直线的倾斜角
,求直线的倾斜角 的值.
的值.
 ,集合
,集合 ,则
,则 等于( )
等于( )



 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 ,
, =( )
=( ) ,则
,则 ( )
( ) 

 ,执行如图所示的程序框图,则输出的
,执行如图所示的程序框图,则输出的 不小于
不小于 的概率为( )
的概率为( )





 ,则
,则 展开式中,
展开式中, 项的系数为( )
项的系数为( )



 在
在 有两个不同的解
有两个不同的解 (
( ),则下面结论正确的是( )
),则下面结论正确的是( )



 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为 ,且有
,且有 ,则
,则 的解集( )
的解集( )



 ,若对任意给定的
,若对任意给定的 ,都存在唯一的
,都存在唯一的 ,满足
,满足 ,则正实数
,则正实数 的最小值是 ( )
的最小值是 ( )



 ,
, ,
, 的夹角为60°,则
的夹角为60°,则 .
. 满足
满足 则
则 的最大值为 .
的最大值为 . 的最小值为 .
的最小值为 .
 为边长为
为边长为 的正方体
的正方体 的内切球,
的内切球, 为球
为球 为
为 中点,
中点, ,则点
,则点 .
. 时,解不等式
时,解不等式 ;
; 的解集为
的解集为 ,
, ,求证:
,求证: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号