高中数学试题

已知函数
（1）讨论的单调性．
（2）证明：（，e为自然对数的底数）

已知函数曲线在点处的切线方程为
（1），求的值；
（2）求证：当时，。

已知椭圆的，离心率为，是其焦点，点在椭圆上。
（Ⅰ）若，且的面积等于。求椭圆的方程；
（Ⅱ）直线交椭圆于另一点，分别过点作直线的垂线，交轴于点，当取最小值时，求直线的斜率。

已知函数
（1）曲线在点处的切线方程为，求的值；
（2）当时，，试求的取值范围。

已知椭圆的，离心率为，是其焦点，点在椭圆上。
（Ⅰ）若，且的面积等于。求椭圆的方程；
（Ⅱ）直线交椭圆于另一点，分别过点作直线的垂线，交轴于点，
当取最小值时，求直线的斜率。

（本小题满分14分）已知直线l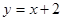：与双曲线C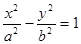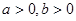：（）相交于B、D两点，且BD的中点为M（1，3）．
（1）求双曲线C的离心率；
（2）设双曲线C的右顶点为A，右焦点为F，，试判断△ABD是否为直角三角形，并说明理由．

（本小题满分14分）已知函数（），．
（1）讨论的单调区间；（2）是否存在时，对于任意的，都有恒成立？若存在，求出m的取值范围；若不存在，请说明理由．

（本小题满分14分）已知直线l：与双曲线C：（）相交于B、D两点，且BD的中点为M（1，3）．
（1）求双曲线C的离心率；
（2）设双曲线C的右顶点为A，右焦点为F，，试判断△ABD是否为直角三角形，并说明理由．

（本小题12分）第（1）小题5分，第（2）题7分
已知中心在原点，左焦点为的椭圆C的左顶点为，上顶点为，到直线的距离为．

（1）求椭圆C的方程；
（2）若椭圆方程为：（），椭圆方程为：（，且），则称椭圆是椭圆的倍相似椭圆．已知是椭圆C的倍相似椭圆，若椭圆C的任意一条切线交椭圆于两点、，试求弦长的取值范围．

（本小题满分12分，（1）小问4分，（2）小问8分）
已知椭圆：的离心率为，且椭圆上一点与椭圆的两个焦点，满足．
（1）求椭圆的方程；
（2）设直线与椭圆交于，两点，且以线段为直径的圆过椭圆的右顶点，求面积的最大值．

已知椭圆的左右焦点分别为，为半焦距，
（1）求椭圆离心率的取值范围；
（2）设椭圆的短半轴长为，以为圆心，为半径作圆，圆与轴的右交点为，过点作倾斜角不为直线与椭圆相交于两点，若，求直线被圆截得的弦长的取值范围。

（本小题12分）如图所示，在平面直角坐标系中，过椭圆内一点的一条直线与椭圆交于点，且，其中为常数．

（1）求椭圆的离心率；
（2）当点恰为椭圆的右顶点时，试确定对应的值；
（3）当时，求直线的斜率．

数列的通项是关于的不等式的解集中正整数的个数，．
（1）求数列的通项公式； （2）若，求数列的前项和；
（3）求证：对且恒有．

（本小题满分12分）已知点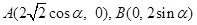（）为平面直角坐标系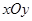中的点，点S为线段AB的中点，当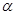变化时，点S形成轨迹．
（1）求S点的轨迹的方程；
（2）若点M的坐标为，是否存在直线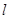交S点的轨迹于P、Q两点，且使点为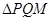的垂心？若存在，求出直线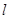的方程；若不存在，请说明理由．

（本小题满分12分）已知点，为平面直角坐标系中的点，点P为线段EF的中点，当变化时，点P形成的轨迹与x轴交于点A，B（A点在左侧），与y轴正半轴交于点C．
（1）求P点的轨迹的方程；
（2）设点M是轨迹上任意一点（不在坐标轴上），直线CM交x轴于点D，直线BM交直线AC于点N．
①若D点坐标为，求线段CM的长；
②求证：为定值．