广东省肇庆市高三第三次统一检测文科数学试卷
已知集合A={-1,0,1},B={1,2},则A∪B=( )
| A.{1} | B.{0,1} | C.{-1,0,2} | D.{-1,0,1,2} |
过抛物线 的焦点F的直线交该抛物线于点A.若|AF|=3,则点A的坐标为( )
的焦点F的直线交该抛物线于点A.若|AF|=3,则点A的坐标为( )
A.(2,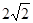 ) B.(2,
) B.(2, )
)
C.(2, ) D.(1,±2)
) D.(1,±2)
如右图是某高三学生进入高中三年来第1次至14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数是 .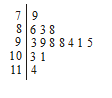
已知W为不等式组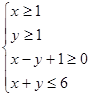 所表示的平面区域,E为圆
所表示的平面区域,E为圆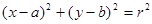 (
(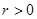 )及其内部所表示的平面区域,若“点
)及其内部所表示的平面区域,若“点 ”是“
”是“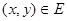 ”的充分条件,则区域E的面积的最小值为 .
”的充分条件,则区域E的面积的最小值为 .
(几何证明选讲选做题)如图,AB是圆O的直径,且AB=6,CD是弦,BA、CD的延长线交于点P,PA=4,PD=5,则∠COD= .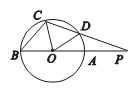
(本小题满分12分)某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如下表.
| |
优秀 |
非优秀 |
总计 |
| 课改班 |
|
50 |
|
| 非课改班 |
20 |
|
110 |
| 合计 |
|
|
210 |
(1)请完成上面的2´2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改
有关”;
(2)若采用分层抽样的方法从课改班的学生中随机抽取4人,则数学成绩优秀和数学成绩非优秀抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求两人数学成绩都优秀的概率.
(本小题满分14分)如图,四棱锥P—ABCD的底面是边长为1的正方形,PD^底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF^PB.
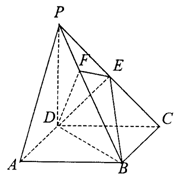
(1)证明:PA//平面EDB;
(2)证明:AC^DF;
(3)求三棱锥B—ADF的体积.
(本小题满分14分)已知数列{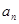 }满足:
}满足: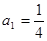 ,
,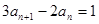 (
( );数列{
);数列{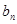 }满足:
}满足: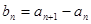 (
( ).
).
(1)求数列{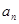 }的通项公式及其前n项和
}的通项公式及其前n项和 ;
;
(2)证明:数列{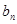 }中的任意三项不可能成等差数列.
}中的任意三项不可能成等差数列.
(本小题满分14分)已知直线l: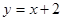 与双曲线C:
与双曲线C: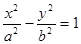 (
(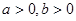 )相交于B、D两点,且BD的中点为M(1,3).
)相交于B、D两点,且BD的中点为M(1,3).
(1)求双曲线C的离心率;
(2)设双曲线C的右顶点为A,右焦点为F, ,试判断△ABD是否为直角三角形,并说明理由.
,试判断△ABD是否为直角三角形,并说明理由.
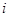 为虚数单位,则复数
为虚数单位,则复数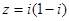 对应的点位于( )
对应的点位于( )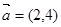 ,
, ,则
,则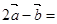 ( )
( )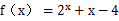 ,则函数
,则函数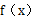 的零点位于区间( )
的零点位于区间( )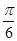

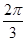
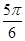
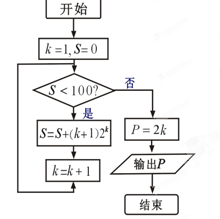
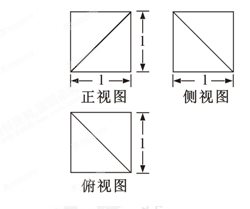
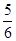
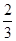
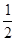
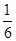
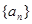 的前n项和为
的前n项和为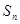 ,若
,若 ,则下列式子中数值不能确定的是( )
,则下列式子中数值不能确定的是( )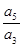
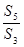
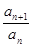
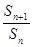
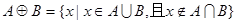 .已知
.已知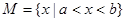 ,
,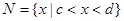 ,其中a、b、c、d满足
,其中a、b、c、d满足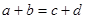 ,
,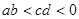 ,则
,则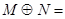 ( )
( )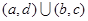 B.
B.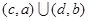
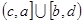 D.
D.
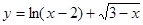 的定义域 .
的定义域 .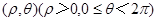 中,点(1,0)关于直线
中,点(1,0)关于直线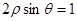 对称的点的极坐标是 .
对称的点的极坐标是 .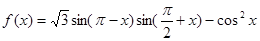 .
.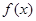 的最小正周期;
的最小正周期;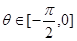 ,
, ,求
,求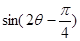 的值.
的值.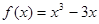 .
.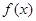 的单调区间;
的单调区间;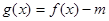 在[
在[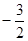 ,3]上有三个零点,求实数m的取值范围;
,3]上有三个零点,求实数m的取值范围;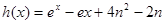 (e为自然对数的底数),如果对任意的
(e为自然对数的底数),如果对任意的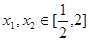 ,都有
,都有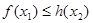 恒成立,求实数n的取值范围.
恒成立,求实数n的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号