期中备考总动员高三理数学模拟卷【山东】7
一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为
①长方形;②正方形;③圆;④椭圆.
| A.①② | B.②③ | C.③④ | D.①④ |
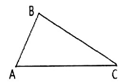
在等腰三角形ABC中,AB=AC,D在线段AC上,AD=kAC(k为常数,且 ),BD=l为定长,则△ABC的面积最大值为
),BD=l为定长,则△ABC的面积最大值为
A. |
B. |
C. |
D. |
学校体育组新买2个同样篮球,3个同样排球,从中取出4个发放给高一4个班,每班1个,则共有______种不同的发放方法.
圆O的半径为1,P为圆周上一点,现将如图放置的边长为1的正方形(实线所示,正方形的顶点A与点P重合)沿圆周逆时针滚动,点A第一次回到点P的位置,则点A走过的路径的长度为_________.
(本小题满分12分)已知函数 的最大值为2,且最小正周期为
的最大值为2,且最小正周期为 .
.
(Ⅰ)求函数 的解析式及其对称轴方程;
的解析式及其对称轴方程;
(Ⅱ)若 的值.
的值.
(本小题满分12分)在如图所示的空间几何体中,平面 平面ABC,
平面ABC, 是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在 的平分线上.
的平分线上.
(Ⅰ)求证:DE//平面ABC;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.
(Ⅰ)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(Ⅱ)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
记 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)已知数列 中,
中,
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)若 是数列
是数列 的前n项和,求满足
的前n项和,求满足 的所有正整数n.
的所有正整数n.
(本小题满分13分) 已知函数 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若对任意 ,不等式
,不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)试探究当 时,方程
时,方程 的解的个数,并说明理由.
的解的个数,并说明理由.





 是实数,则实数t等于
是实数,则实数t等于



 ,则
,则

 的最大值是最小值的4倍,则
的最大值是最小值的4倍,则 的值是
的值是




 则满足
则满足 的实数a的取值范围是
的实数a的取值范围是



 的导函数为
的导函数为 ,当
,当 时,
时, ,若
,若 ,则
,则 的大小关系正确的是
的大小关系正确的是



 的离心率为2,则
的离心率为2,则 ________.
________. ,则
,则 ______.
______. 中,若
中,若 ______.
______.
 ,其中
,其中 为左、右焦点,O为坐标原点.直线l与椭圆交于
为左、右焦点,O为坐标原点.直线l与椭圆交于 两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
两个不同点.当直线l过椭圆C右焦点F2且倾斜角为 时,原点O到直线l的距离为
时,原点O到直线l的距离为 .又椭圆上的点到焦点F2的最近距离为
.又椭圆上的点到焦点F2的最近距离为 .
.
 时,求平行四边形OQNP的对角线之积
时,求平行四边形OQNP的对角线之积 的最大值;
的最大值; 为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标. 粤公网安备 44130202000953号
粤公网安备 44130202000953号