如下图,在正三棱柱 中, ,D是 的中点,点E在 上,且 。

(1)证明:平面 平面
(2)求直线 和平面 所成角的正弦值。
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的 、 、 ,现在3名工人独立地从中任选一个项目参与建设。
(1)求他们选择的项目所属类别互不相同的概率;
(2)记 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求 的分布列及数学期望。
已知函数 , M为不等式 的解集.
(1)求 ;
(2)证明:当 时, 。
在直线坐标系 中,圆 C的方程为 .
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求 C的极坐标方程;
(2)直线 l的参数方程是 , l与 C交于 A、 B两点, ,求 l的斜率。
如图,在正方形 , 分别在边 上(不与端点重合),且 ,过D点作 , 垂足为F.
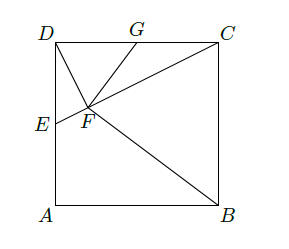
(1)证明: 四点共圆;
(2)若 ,E为DA的中点,求四边形BCGF的面积.
(1)讨论函数 的单调性,并证明当 >0时,
(2)证明:当 时,函数 有最小值.设 的最小值为 ,求函数 的值域.
已知椭圆 的焦点在 轴上, A是 E的左顶点,斜率为 的直线交 E于 A, M两点,点 N在 E上, .
(1)当 , 时,求 的面积;
(2)当 时,求 k的取值范围.
如图,菱形ABCD的对角线 与 交于点 , , ,点 分别在 上, , 交 于点 .将 沿 折到 的位置, .
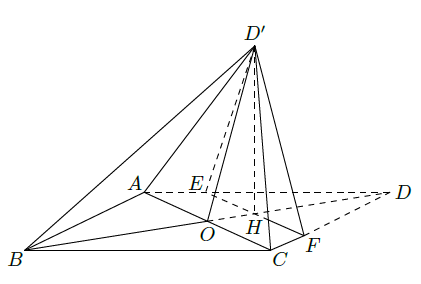
(1)证明: 平面 ;
(2)求二面角 的正弦值.
某险种的基本保费为 (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 |
0 |
1 |
2 |
3 |
4 |
5 |
保费 |
0.85a |
a |
1.25a |
1.5a |
1.75a |
2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 |
0 |
1 |
2 |
3 |
4 |
5 |
概率 |
0.30 |
0.15 |
0.20 |
0.20 |
0.10 |
0. 05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.
为等差数列 的前n项和,且 记 ,其中 表示不超过x的最大整数,如 .
(1)求 ;
(2)求数列 的前1 000项和.
设函数 ,其中 。
(1)求 的单调区间;
(2)若 存在极点 , 且 ,其中 , 求证: ;
(3)设 ,函数 ,求证: 在区间 上的最大值不小于 .
设椭圆 的右焦点为F,右顶点为A,已知 ,其中O为原点,e为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点A的直线l与椭圆交于B(B不在 轴上),垂直于l的直线与l交于点M,与y轴交于点H,若 ,且 ,求直线 的斜率.
已知 是各项均为整数得等差数列,公差为d,对任意的 , 是 和 得等比中项。
(1)设 , ,求证:数列 是等差数列;
(2)设 , , ,求证: