高中数学解答题

（本小题满分15分）
某地建一座桥，两端的桥墩已建好，这两墩相距米，余下工程只需要建两端桥墩之间的桥面和桥墩，经预测，一个桥墩的工程费用为256万元，距离为米的相邻两墩之间的桥面工程费用为万元。假设桥墩等距离分布，所有桥墩都视为点，且不考虑其他因素，记余下工程的费用为万元。
（Ⅰ）试写出关于的函数关系式；
（Ⅱ）当=640米时，需新建多少个桥墩才能使最小？

（本小题14分）某企业生产A、B两种产品，根据市场调查与预测，A产品的利润与投资成正比，其关系如左图， B产品的利润与投资的算术平方根成正比，其关系如右图 (注：利润与投资单位：万元)．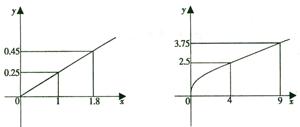

(1)分别将A、B两种产品的利润表示为投资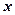(万元)的函数关系式；
(2)该企业已筹集到10万元资金，并全部投入A、B两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大利润为多少万元?

（本小题14分）已知函数f(x)=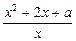,x∈［1,+∞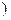
(1)当a=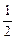时，求函数f(x)的最小值
(2)若对任意x∈［1,+∞,f(x)>0恒成立，试求实数a的取值范围
（3）求f(x)的最小值

已知,函数.
(1) 如果实数满足,函数是否具有奇偶性？如果有,求出相应的值,如果没有，说明为什么?
(2) 如果判断函数的单调性；
(3) 如果，，且，求函数的对称轴或对称中心.

(本小题满分16分)如图，、是通过某城市开发区中心的两条南北和东西走向的街道，连接、两地之间的铁路线是圆心在上的一段圆弧．若点在点正北方向，且，点到、的距离分别为和．
（1）建立适当坐标系，求铁路线所在圆弧的方程；
（2）若该城市的某中学拟在点正东方向选址建分校,考虑环境问题，要求校址到点的距离大于，并且铁路线上任意一点到校址的距离不能少于，求该校址距点O的最近距离（注：校址视为一个点）．

已知命题：方程有两个不等的负实根；命题：方程无实根，若“p或q”为真命题，“p且q”为假命题，求实数m的取值范围

如图所示，直三棱柱,底面中，,棱分别是的中点.
(1)    求的长；
(2)    求异面直线所成角的余弦值.

若 P为椭圆上任意一点，为左、右焦点，

(1)若的中点为M，求证：；
(2)若，求之值；
(3)椭圆上是否存在点P，使，若存在，求出P点的坐标，
若不存在，请说明理由。

已知一条曲线C在y轴右边，C上每一点到点F（1，0）的距离减去它到y轴距离的差都是1.
（1）求曲线C的方程；
（2）是否存在正数m, 对于过点M（m,0）且与曲线C有两个交点A,B的任一直线，都有
  若存在，求出m的取值范围；若不存在，请说明理由。

已知函数是增函数，为减函数.
（1）求a的值；
（2）设函数上的增函数，且对于内的任意两个变量s、t，恒成立，求实数b的取值范围；
（3）设，求证：

如图，P—ABCD是正四棱锥，是正方体，其中 
（1）求证：；
（2）求平面PAD与平面所成的锐二面角的余弦值；
（3）求到平面PAD的距离

已知椭圆，直线与椭圆交于A、B两点，M是线段AB的中点，连接OM并延长交椭圆于点C．直线AB与直线OM的斜率分别为k、m，且．
（1）求的值；
(2）若直线AB经过椭圆的右焦点F，问：对于任意给定的不等于零的实数k，是否存在a∈，使得四边形OACB是平行四边形，请证明你的结论；

已知动圆C过点A(－2，0)，且与圆相内切。
(1)求动圆C的圆心的轨迹方程；
(2)设直线: y=kx+m(其中k，m∈Z)与(1)所求轨迹交于不同两点B，D，与双曲线交于不同两点E，F，问是否存在直线，使得向量，若存在，指出这样的直线有多少条？若不存在，请说明理由

若向量，在函数的图象中，对称中心到对称轴的最小距离为且当的最大值为1。
（I）求函数的解析式；
（II）求函数的单调递增区间。

如图，已知椭圆的上顶点为,右焦点为,直线与圆相切.
（Ⅰ）求椭圆的方程；
（Ⅱ）若不过点的动直线与椭圆相交于、两点，且求证：直线过定点，并求出该定点的坐标