高中数学解答题

已知，函数(R).
（1）求；     (2)求的最小正周期和最大值；
（3）若为锐角，且，求的值

(本小题满分12分)

	喜爱打篮球	不喜爱打篮球	合计
男生		5
女生	10
合计:			５０

为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为．
（1）请将上面的列联表补充完整；
（2）是否有99.5％的把握认为喜爱打篮球与性别有关？说明你的理由；
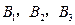（3）已知喜爱打篮球的10位女生中，还喜欢打羽毛球，还喜欢打乒乓球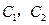，还喜欢踢足球，现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查，求女生和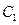不全被选中的概率．
下面的临界值表供参考：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：，其中.）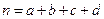

如图，在四棱锥中，底面ABCD是正方形，侧棱底面ABCD，PD=DC，E是PC的中点，作交于点F。
证明：（Ⅰ）平面EDB；
（Ⅱ）平面EFD。

（本小题满分12分）
已知向量，，函数
（1）若，求的值；
（2）在△ABC中，角A，B，C的对边分别是，且满足，求的取值范围．

在△ABC中，角A，B，C所对的边分别为a,b,c,设S为△ABC的面积，满足。
（Ⅰ）求角C的大小；
（Ⅱ）求的最大值。

已知椭圆：的离心率为，过坐标原点且斜率为的直线与相交于、，．
⑴求、的值；
⑵若动圆与椭圆和直线都没有公共点，试求的取值范围．

某商场销售某种商品的经验表明，该商品每日的销售量y（单位一：千克）与销售价格x（单位：元/千克）满足关系式其中，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克。
（1）求a的值
（2）若该商品的成本为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大

若向量，其中，设函数，其周期为，且是它的一条对称轴。
（1）    求的解析式；
（2）    当时，不等式恒成立，求实数a的取值范围。

数列的前项和为，且，试求：
（1）的值；
（2）数列的通项公式；
（3）的值。

如图，P—ABCD是正四棱锥，是正方体，其中
（1）求证：；
（2）求平面PAD与平面所成的锐二面角的余弦值；
（3）求到平面PAD的距离

已知动圆C过点A(－2，0)，且与圆相内切。
(1)求动圆C的圆心的轨迹方程；
(2)设直线: y=kx+m(其中k，m∈Z)与(1)所求轨迹交于不同两点B，D，与双曲线交于不同两点E，F，问是否存在直线，使得向量，若存在，指出这样的直线有多少条？若不存在，请说明理由.

设命题：，命题：；如果“或”为真，“且”为假，求的取值范围。

由世界自然基金会发起的“地球1小时”活动，已发展成为最有影响力的环保活动之一，今年的参与人数再创新高。然而也有部分公众对该活动的实际效果与负面影响提出了疑问。对此，某新闻媒体进行了网上调查，所有参与调查的人中，持“支持”、“保留”和“不支持”态度的人数如下表所示：

	支持	保留	不支持
20岁以下	800	450	200
20岁以上（含20岁）	100	150	300

⑴在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持”态度的人中抽取了45个人，求n的值；
⑵在持“不支持”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中
任意选取2人，求至少1人20岁以下的概率；
⑶在接受调查的人中，有8人给这项活动打出了分数如下：9.4， 8.6, 9.2, 9.6, 8.7
9.3， 9.0， 8.2.把这8人打出的分数看作一个总体，从中任取一个数，求该数与总体平均数之差的绝对值超过0.6的概率。

如图，在三棱锥中，，，点分别是的中点，底面．
（1）求证：平面；
（2）当时，求直线与平面所成角的余弦值；
（3）当为何值时，在平面内的射影恰好为的重心？

已知数列的各项均为正数，观察程序框图，若时，分别有.
(1)试求数列的通项；
(2)令，求的值.