高中数学解答题

（本小题满分12分）
已知在四棱锥中，底面是边长为4的正方形，平面⊥平面，△是正三角形， 、、分别是、、的中点．
（I）求证：平面；
（II）求平面与平面所成锐二面角的大小.

设函数为实数。
（Ⅰ）已知函数在处取得极值，求的值；
（Ⅱ）已知不等式对任意都成立，求实数的取值范围。

某地有三个村庄，分别位于等腰直角三角形ABC的三个顶点处，已知AB=AC=6km，现计划在BC边的高AO上一点P处建造一个变电站．记P到三个村庄的距离之和为y.
（1）设，求y关于的函数关系式；
（2）变电站建于何处时，它到三个小区的距离之和最小？

某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本为C(x)，年
产量不足80千件时，C(x)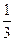＝²＋10x(万元)；当年产量不小于80千件时，
C(x)＝51x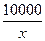＋－1450(万元)．通过市场分析，若每件售价为500元时，该厂当年生产
的该产品能全部销售完．
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式；
(2)年产量为多少千件时，该厂在这一产品的生产中所获利润最大，最大利润是多少？

（本小题满分13分）
如图，四边形为正方形，⊥平面，∥，==．
（I）证明：平面⊥平面；
（II）求二面角的余弦值．

(本小题满分12分已知二次函数f(x) 对任意x∈R，都有f (1-x)="f" (1+x)成立，设向量a="(sinx,2)," b=(2sinx,),
c=(cos2x,1),d=(1,2)。
（1）分别求a·b和c·d的取值范围；
（2）当x∈[0,π]时，求不等式f(a·b)>f(c·d)的解集.

（本小题满分14分）
如图所示，在棱长为2的正方体中，、分别为、的中点．
（1）求证：//平面；
（2）求证：；
（3）求三棱锥的体积．

（本小题12分）一个盒子中装有张卡片，每张卡片上写有个数字，数字分别是、、、。现从盒子中随机抽取卡片，
⑴若一次抽取张卡片，求张卡片上数字之和大于的概率；
⑵若第一次抽张卡片，放回后再抽取张卡片，求两次抽取中至少一次抽到数字的概率。

（本小题12分）
⑴焦点在y轴上的椭圆的一个顶点为A（2，0），其长轴长是短轴长的2倍，求椭圆的标准方程。
⑵已知双曲线的一条渐近线方程是，并经过点，求此双曲线的标准方程。

（本小题12分）
如图4：求的算法的
程序框图。⑴标号①处填       。标号②处填       。⑵根据框图用直到型（UNTIL）语句编写程序。

（本小题满分12分）
不用计算器计算：
（Ⅰ）  
（Ⅱ）设求的值；

已知向量，设函数。
（1）求的最小正周期与单调递减区间。
（2）在中，、、分别是角、、的对边，若的面积为，求的值

（本小题14分）
已知椭圆的一个顶点为，离心率．
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线l与椭圆交于A，B两点，坐标原点O到直线l的距离为，
求△AOB面积的最大值．

（本小题14分）
已知函数，
（Ⅰ）求；
（Ⅱ）已知数列满足，，求数列的通项公式；
（Ⅲ）求证：．

在直角坐标系中，点到两点、的距离之和等于4，设点的轨迹为曲线，直线与曲线交于、两点.
（1）求出的方程；
（2）若=1，求的面积；
（3）若OA⊥OB，求实数的值。