高中数学解答题

已知向量，，函数，．
（Ⅰ）求函数的最小正周期；
（Ⅱ）在中，分别是角的对边，且，，，且，求的值．

某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上40件产品作为样本，称出它们的重量（单位：克），重量的分组区间为，，…，，由此得到样本的频率分布直方图，如右图所示．
（1）根据频率分布直方图，求重量超过505克的产品数量．
（2）在上述抽取的40件产品中任取2件，设为重量超过505克的产品数量，求的分布列．
（3）从流水线上任取5件产品，求恰有2件产品的重量超过505克的概率

．(本题满分14分）
设命题p:函数的定义域为R;
命题不等式恒成立
如果命题“”为真命题，且“”为假命题，求实数的取值范围

某省两相近重要城市之间人员交流频繁，为了缓解交通压力，特修一条专用铁路，用一列火车作为交通车，已知该车每次拖4节车厢，一日能来回16次， 如果每次拖7节车厢，则每日能来回10次．
（1）若每日来回的次数是车头每次拖挂车厢节数的一次函数，求此一次函数解析式；
（2）在（1）的条件下，每节车厢能载乘客110人．问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。

（本小题满分12分）已知命题，命题，若是真命题，是假命题，求实数的取值范围。

（本小题满分10分）
写出“若，则”的逆命题、否命题、逆否命题，并判其真假.

（本小题满分12分）
已知椭圆的中心在坐标原点，焦点在轴上，椭圆的短轴端点和焦点所组成的四边形为正方形，短轴长为2．
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线过且与椭圆相交于A，B两点，当P是AB的中点时，
求直线的方程．

设命题：，命题：；
如果“或”为真，“且”为假，求的取值范围。（在数学中“所有”一词，叫全称量词，用符号“”表示；“存在”一词，叫做存在量词，用符号“”表示）

从一箱产品中随机地抽取一件产品,设事件A=“抽到的一等品”,事件B=“抽到的二等品”,事件C=“抽到的三等品”,且已知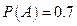,,,求下列事件的概率：⑴ 事件D=“抽到的是一等品或二等品”；⑵ 事件E=“抽到的是二等品或三等品” ．

由世界自然基金会发起的“地球1小时”活动，已发展成为最有影响力的环保活动之一，今年的参与人数再创新高。然而也有部分公众对该活动的实际效果与负面影响提出了疑问。对此，某新闻媒体进行了网上调查，所有参与调查的人中，持“支持”、“保留”和“不支持”态度的人数如下表所示：

	支持	保留	不支持
20岁以下	800	450	200
20岁以上（含20岁）	100	150	300

⑴在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持”态度的人中抽取了45个人，求n的值；
⑵在持“不支持”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中
任意选取2人，求至少1人20岁以下的概率；
⑶在接受调查的人中，有8人给这项活动打出了分数如下：9.4， 8.6, 9.2, 9.6, 8.7
9.3， 9.0， 8.2.把这8人打出的分数看作一个总体，从中任取一个数，求该数与总体平均数之差的绝对值超过0.6的概率。

已知四棱锥的底面为直角梯形，，底面，且，
，是的中点。
（1）证明：面面；
（2）求与所成的角的余弦值；
（3）求面与面所成二面角的正切值。

如图①在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2，E，F，G分别是线段PC、PD，BC的中点，现将ΔPDC折起，使平面PDC⊥平面ABCD（如图②）
（1）求证AP∥平面EFG；
（2）求直线AP与平面EFG之间的距离；
（3）在线段PB上确定一点Q，使PC⊥平面ADQ，试给出证明．

. 根据如图所示的程序框图，将输出的x、y值依次分别
记为y₁，y₂，…，y_n，…，y₂₀₀₇
（1）求数列的通项公式；
（2）写出y₁，y₂，y₃，y₄，由此猜想出数列{y_n}的一个
通项公式y_n，并证明你的结论；
（3）求

（本小题满分12分）已知函数.
(1)确定函数f(x)的单调增区间；
(2)将函数y=f(x)的图象向左平移个单位长度，所得图象关于y轴对称，求φ的值。

（本小题满分12分）已知，，且// ．设函数．
（1）求函数的解析式；
（2）若在锐角中，，边，求周长的最大值．