高中数学解答题

在平面直角坐标系中，已知矩形的长为２，宽为１，边分别在ｘ轴、ｙ轴的正半轴上，点与坐标原点重合（如图4所示），将矩形折叠，使点落在线段上.
（Ⅰ）若折痕所在直线的斜率为，试写出折痕所在直线的方程；
（Ⅱ）设折痕线段为EF，记，求的解析式.

设数列中，（c为常数，），且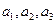是公比不为1的等比数列。
（1）求c的值；
（2）求数列的通项公式

（本小题满分12分）函数的定义域为集合A，关于x的不等式的解集为B，求使的实数的取值范围。

（本小题满分12分）
某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房．经测算，如果将楼房建为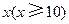层，则每平方米的平均建筑费用为（单位：元）．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用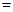平均建筑费用平均购地费用，平均购地费用）

（本小题满分14分）
已知数列的前n项和与通项之间满足关系
（I）求数列的通项公式；
（II）设求
（III）若，求的前n项和

已知函数的图象关于原点成中心对称, 试判断在区间上的单调性,并证明你的结论.

(1) 化简 （4分 ）
(2) 求函数的定义域和值域.

(本小题满分12分)
在中，角所对的边分别为且满足
（I）求角的大小；
（II）求的最大值，并求取得最大值时角的大小．

某工厂生产一种产品的成本费由三部分组成：① 职工工资固定支出元；② 原材料费每件40元；③ 电力与机器保养等费用为每件元，其中是该厂生产这种产品的总件数.
（1）把每件产品的成本费P(x)（元）表示成产品件数的函数，并求每件产品的最低成本费；
（2）如果该厂生产的这种产品的数量不超过件，且产品能全部销售．根据市场调查：每件产品的销售价与产品件数有如下关系：，试问生产多少件产品，总利润最高？（总利润=总销售额—总的成本）

已知全集为，集合
求：（１）（２）；（３）

（此题10分）已知，且
求的值
判断函数的奇偶性
判断函数在上的单调性，并加以证明

在中，已知内角A、B、C所对的边分别为a、b、c，
向量， ,且
（I）求锐角B的大小；   
（II）如果，求的面积的最大值。

(本小题满分12分) (Ⅰ)小问7分，(Ⅱ)小问5分.)
已知O为坐标原点，向量＝(sinα，1)，＝(cosα，0)，＝(－sinα，2)，点P是直线AB上的一点，且点B分有向线段的比为1.
(1)记函数f(α)＝·，α∈，讨论函数f(α)的单调性，并求其值域；
(2)若O、P、C三点共线，求|＋|的值．

（本小题满分12分）已知函数，
且函数的最小正周期为
（1）若，求函数的单调递减区间；
（2）将函数的图象上各点的纵坐标保持不变，横坐标缩短到原来的，把所得到的图象再向左平移个单位，得到函数的图象，求函数在区间上的最小值。

（本小题满分12分）
已知向量
（1）求a·b及|a+b|；
（2）若的最小值是，求实数的值。