在平面直角坐标系中,已知矩形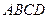 的长为2,宽为1,
的长为2,宽为1,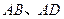 边分别在x轴、y轴的正半轴上,
边分别在x轴、y轴的正半轴上,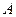 点与坐标原点重合(如图4所示),将矩形折叠,使
点与坐标原点重合(如图4所示),将矩形折叠,使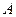 点落在线段
点落在线段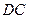 上.
上.
(Ⅰ)若折痕所在直线的斜率为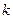 ,试写出折痕所在直线的方程;
,试写出折痕所在直线的方程;
(Ⅱ)设折痕线段为EF,记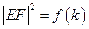 ,求
,求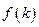 的解析式.
的解析式.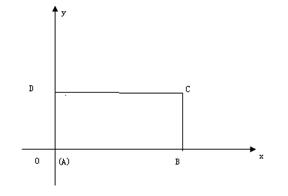
推荐套卷
在平面直角坐标系中,已知矩形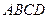 的长为2,宽为1,
的长为2,宽为1,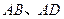 边分别在x轴、y轴的正半轴上,
边分别在x轴、y轴的正半轴上,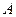 点与坐标原点重合(如图4所示),将矩形折叠,使
点与坐标原点重合(如图4所示),将矩形折叠,使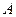 点落在线段
点落在线段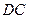 上.
上.
(Ⅰ)若折痕所在直线的斜率为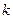 ,试写出折痕所在直线的方程;
,试写出折痕所在直线的方程;
(Ⅱ)设折痕线段为EF,记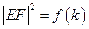 ,求
,求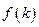 的解析式.
的解析式.