已知椭圆
，直线
与椭圆交于A、B两点，M是线段AB的中点，连接OM并延长交椭圆于点C．直线AB与直线OM的斜率分别为k、m，且
．
（1）求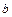
的值；
(2）若直线AB经过椭圆的右焦点F，问：对于任意给定的不等于零的实数k，是否存在a∈
，使得四边形OACB是平行四边形，请证明你的结论；
相关试题
的图象
关于原点对称，
，
为实数，
在
上是减函数；
时，不等式
恒成立，求实数
的取值范围。
的前
项和
满足：
；设
，求数列
的前
的方程为
。
，求
的取值范围。
的最大值和最小值。推荐套卷
已知椭圆，直线与椭圆交于A、B两点，M是线段AB的中点，连接OM并延长交椭圆于点C．直线AB与直线OM的斜率分别为k、m，且．
（1）求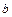的值；
(2）若直线AB经过椭圆的右焦点F，问：对于任意给定的不等于零的实数k，是否存在a∈，使得四边形OACB是平行四边形，请证明你的结论；
粤公网安备 44130202000953号