在每道单项选择题给出的4个备选答案中,只有一个是正确的.若对4道选择题中的每一道都任意选定一个答案,求这4道题中:
(Ⅰ)恰有两道题答对的概率;
(Ⅱ)至少答对一道题的概率.
设 的内角 , , 的对边分别为 , , .已知 ,求:
(Ⅰ) 的大小;
(Ⅱ) 的值.
若 是抛物线 上的不同两点, 弦 (不平行于 轴)的垂直平分线与 轴相交于点 , 则称弦 是点 的一条 "相关弦".已知当 时,点
存在无穷多条 "相关弦" .给定 .
(I) 证明:点 的所有"相关弦"的中点的横坐标相同;
(II) 试问:点 的"相关弦"的弦长中是否存在最大值?若存在, 求其最大值(用 表示):若不存在, 请说明理由.
在一个特定时段内, 以点 为中心的7海里以内海域被设为警戒水域.点 正北55海里处有一个 雷达观测站 .某时刻测得一艘匀速直线行驶的船只位于点 北偏东 且与点 相距 海里的位置 ,经过40分钟又测得该船已行驶到点 北偏东 (其中 )且与点 相距 海里的位置C.
(Ⅰ)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
如图所示,四棱锥 的底面 是边长为 1 的菱形, , 是 的中点, 底面 .
(I) 证明: 平面 平面 ;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的大小.

甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约.甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是 , 且面试是否合格互不影响.
求: ( I ) 至少有 1 人面试合格的概率;
( II ) 签约人数 的分布列和数学期望.
已知函数 .
(1)设 .
①求方程 的根;
②若对任意 , 不等式 恒成立, 求实数 的最大值;
(2)若 , 函数 有且只有 1 个零点, 求 的值。
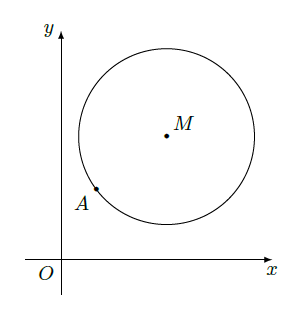
如图, 在平面直角坐标系 中, 已知以 为圆心的圆
及其上一点
(1) 设圆 与 轴相切, 与圆 外切, 且圆心 在直线 上, 求圆 的标准方程;
(2) 设平行于 的直线 与圆 相交于 两点, 且 , 求直线 的方程;
(3) 设点 满足:存在圆 上的两点 和 , 使得 , 求实数 的取值范围。
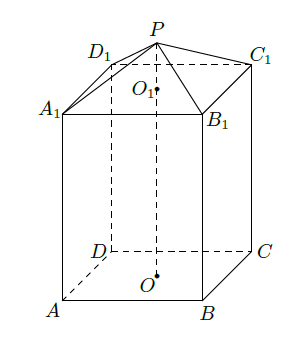
现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱雉 ,下部分的形状是正四棱柱 (如图所示),并要求正四棱柱的高 的四倍.
(1)若 ,则仓库的容积是多少?
(2)若正四棱柱的侧棱长为 ,则当 为多少时,仓库的容积最大?
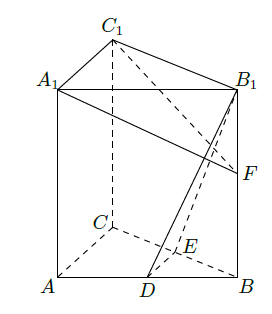
如图,在直三棱柱 中, 分别为 的中点,点 在侧棱 上, 且
求证:(1)直线 平面 ;
(2) 平面 平面 ;