设 为数列 的前 n项和, ,其中 是常数.
(Ⅰ)求 及 ;
(Ⅱ)若对于任意的 , , , 成等比数列,求 k的值.
如图, , , , ,P,Q分别为AE,AB的中点.

(Ⅰ)证明: ;
(Ⅱ)求 与 所成角的正弦值.
在 中,角A,B,C所对的边分别为a,b,c,且满足 , .
(Ⅰ)求 的面积;
(Ⅱ)若 ,求 的值.
双曲线 ,圆 在第一象限交点为A, ,曲线 。
(1)若 ,求b;
(2)若 , 与x轴交点记为 ,P是曲线 上一点,且在第一象限,并满足 ,求∠ ;
(3)过点 且斜率为 的直线 交曲线 于M、N两点,用b的代数式表示 ,并求出 的取值范围。

已知: , ,且 ,
(1)若v>95,求x的取值范围;
(2)已知x=80时,v=50,求x为多少时,q可以取得最大值,并求出该最大值。
已知 .
(1)若f(x)的周期是4π,求 ,并求此时 的解集;
(2)已知 , , ,求g(x)的值域.
已知边长为1的正方形ABCD,沿BC旋转一周得到圆柱体。
(1)求圆柱体的表面积;
(2)正方形ABCD绕BC逆时针旋转 到 ,求 与平面ABCD所成的角。

已知双曲线 的离心率为 ,右准线方程为
(Ⅰ)求双曲线 的方程;
(Ⅱ)设直线 是圆 上动点 处的切线, 与双曲线 交于不同的两点 ,证明 的大小为定值。
设函数
(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)求函数 的单调区间;
(Ⅲ)若函数 在区间 内单调递增,求 的取值范围。
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min。
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间 的分布列及期望。
如图,在三棱锥 中, 底面 ,点 , 分别在棱 上,且

(Ⅰ)求证: 平面 ;
(Ⅱ)当 为 的中点时,求 与平面 所成的角的大小;
(Ⅲ)是否存在点 使得二面角 为直二面角?并说明理由。
如图, 和 是平面上的两点,动点 满足:
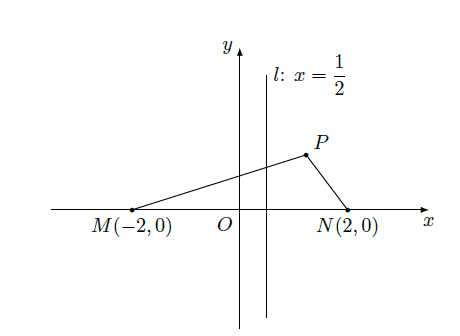
(Ⅰ)求点 的轨迹方程;
(Ⅱ)设 为点 到直线 : 的距离,若 ,求 的值.
如图,  为平面,
,
,
在棱
上的射影分别为
,
,
,
.若二面角
的大小为
,求:
为平面,
,
,
在棱
上的射影分别为
,
,
,
.若二面角
的大小为
,求:

(Ⅰ)点 到平面 的距离;
(Ⅱ)异面直线 与 所成的角(用反三角函数表示).