在平面直角坐标系 中, 的参数方程为 ( 为参数),过点 且倾斜角为 的直线 与 交于 两点.
(1)求 的取值范围;
(2)求 中点 的轨迹的参数方程.
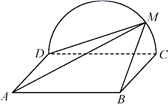
如图,矩形 所在平面与半圆弧 所在平面垂直, 是 上异于 , 的点.
(1)证明:平面 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ?说明理由.
某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
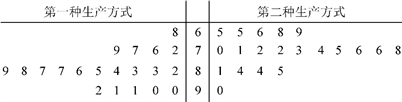
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数 ,并将完成生产任务所需时间超过 和不超过 的工人数填入下面的列联表:
| |
超过 |
不超过 |
| 第一种生产方式 |
|
|
| 第二种生产方式 |
|
|
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附: ,
| |
|
|
|
| |
|
|
|
如图,在极坐标系 中, , , , ,弧 , , 所在圆的圆心分别是 , , ,曲线 是弧 ,曲线 是弧 ,曲线 是弧 .
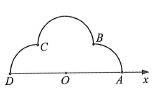
(1)分别写出 , , 的极坐标方程;
(2)曲线 由 , , 构成,若点 在 上,且 ,求 的极坐标.
已知曲线 C: y= , D为直线 y= 上的动点,过 D作 C的两条切线,切点分别为 A, B.
(1)证明:直线 AB过定点:
(2)若以 E(0, )为圆心的圆与直线 AB相切,且切点为线段 AB的中点,求四边形 ADBE的面积.
已知函数 .
(1)讨论 的单调性;
(2)是否存在 ,使得 在区间 的最小值为 且最大值为1?若存在,求出 的所有值;若不存在,说明理由.
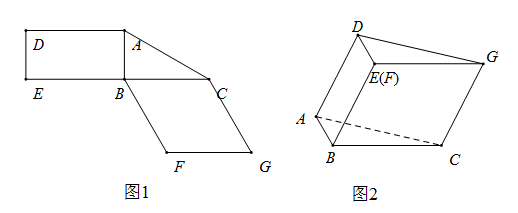
图1是由矩形 ADEB,Rt△ ABC和菱形 BFGC组成的一个平面图形,其中 AB=1, BE= BF=2,∠ FBC=60°,将其沿 AB, BC折起使得 BE与 BF重合,连结 DG,如图2.
(1)证明:图2中的 A, C, G, D四点共面,且平面 ABC⊥平面 BCGE;
(2)求图2中的二面角 B−CG−A的大小.
的内角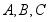 的对边分别为
,已知
.
的对边分别为
,已知
.
(1)求 ;
(2)若 为锐角三角形,且 ,求 面积的取值范围.
如图,已知点 为抛物线 的焦点,过点 的直线交抛物线于 两点,点 在抛物线上,使得 的重心 在 轴上,直线 交 轴于点 ,且 在点 右侧.记 的面积为 .

(1)求 的值及抛物线的准线方程;
(2)求 的最小值及此时点 的坐标.
设等差数列 的前 项和为 , , ,数列 满足:对每 成等比数列.
(1)求数列 的通项公式;
(2)记 证明:
如图,已知三棱柱 ,平面 平面 , , 分别是 的中点.

(1)证明: ;
(2)求直线 与平面 所成角的余弦值.
在直角坐标系xOy中,曲线C的参数方程为 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
(1)求C和l的直角坐标方程;
(2)求C上的点到l距离的最小值.
已知点A,B关于坐标原点O对称,│AB│ =4,⊙M过点A,B且与直线x+2=0相切.
(1)若A在直线x+y=0上,求⊙M的半径.
(2)是否存在定点P,使得当A运动时,│MA│-│MP│为定值?并说明理由.