如图,三棱柱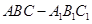 中,侧棱
中,侧棱 平面
平面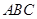 ,
,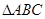 为等腰直角三角形,
为等腰直角三角形,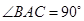 ,且
,且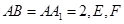 分别是
分别是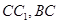 的中点.
的中点.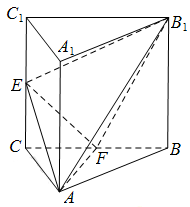
(1)求证: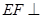 平面
平面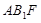 ;
;
(2)求锐二面角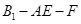 的余弦值;
的余弦值;
(3)若点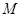 是
是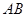 上一点,求
上一点,求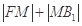 的最小值.
的最小值.
函数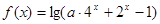
(1)如果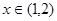 时,
时,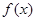 有意义,确定
有意义,确定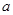 的取值范围;
的取值范围;
(2)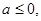 若
若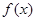 值域为
值域为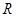 ,求
,求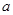 的值;
的值;
(3)在(2)条件下,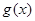 为定义域为
为定义域为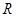 的奇函数,且
的奇函数,且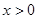 时,
时,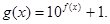 对任意的
对任意的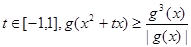 恒成立,求
恒成立,求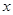 的取值范围.
的取值范围.
设a,b,c分别是△ABC中角A,B,C的对边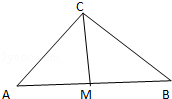
(1)若AB边上的中线CM=AB=2,求a+b的最大值;
(2)若AB边上的高h=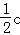 ,求
,求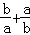 的取值范围.
的取值范围.
要使函数y=1+2x+4xa在x∈(﹣∞,﹣1]时,y>0恒成立,求实数a的取值范围.
(1)计算:(2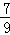 )
)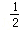 +(lg5)0+(
+(lg5)0+(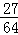 )
) ;
;
(2)解方程:log3(6x﹣9)=3.
已知函数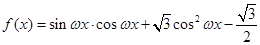
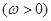 ,直线
,直线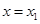 ,
, 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且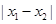 的最小值为
的最小值为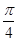 .
.
(1)求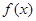 的表达式;
的表达式;
(2)将函数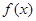 的图象向右平移
的图象向右平移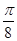 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐
标不变,得到函数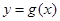 的图象,若关于
的图象,若关于 的方程
的方程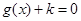 ,在区间
,在区间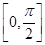 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数 的取值范围.
的取值范围.
如图,三棱柱 中,侧棱
中,侧棱 平面
平面 ,
, 为等腰直角三角形,
为等腰直角三角形,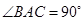 ,且
,且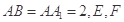 分别是
分别是 的中点.
的中点.
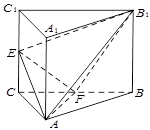
(1)求证: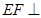 平面
平面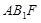 ;
;
(2)求三棱锥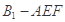 的体积.
的体积.
(3)若点 是
是 上一点,求
上一点,求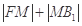 的最小值.
的最小值.
已知中心在原点,焦点在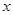 轴的椭圆过点
轴的椭圆过点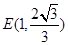 ,且焦距为2,过点
,且焦距为2,过点 分别作斜率为
分别作斜率为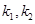 的椭圆的动弦
的椭圆的动弦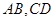 ,设
,设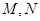 分别为线段
分别为线段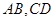 的中点.
的中点.
(1)求椭圆的标准方程;
(2)若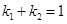 ,求证:直线
,求证:直线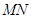 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
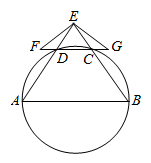
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且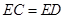 .
.
(1)证明: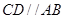 ;
;
(2)延长CD到F,延长DC到G,使得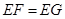 ,证明:A,B,G,F四点共圆.
,证明:A,B,G,F四点共圆.
[选修4—2:矩阵与变换]
已知矩阵 ,求矩阵
,求矩阵 的特征值和特征向量.
的特征值和特征向量.