(本小题满分10分)【选修4一1:几何证明选讲】
如图,已知圆的两条弦AB, CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证: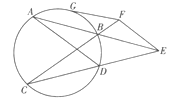
(1)△EFC∽△BFE;
(2)FG=FE
(本小题满分12分)已知椭圆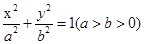 经过点A(0,4),离心率为
经过点A(0,4),离心率为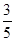 ;
;
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为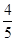 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
(本小题满分10分)
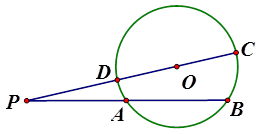
自圆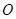 外一点
外一点 引圆
引圆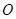 的两条割线
的两条割线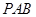 和
和 ,如图所示,其中割线
,如图所示,其中割线 过圆心
过圆心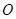 ,
,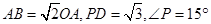 .
.
(1)求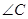 的大小;
的大小;
(2)分别求线段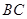 和
和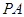 的长度.
的长度.
(本小题满分10分)
已知在直角坐标系 中,圆
中,圆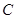 的参数方程为
的参数方程为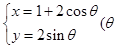 为参数).
为参数).
(1)以原点为极点、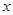 轴正半轴为极轴建立极坐标系,求圆
轴正半轴为极轴建立极坐标系,求圆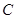 的极坐标方程;
的极坐标方程;
(2)直线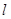 的坐标方程是
的坐标方程是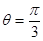 ,且直线
,且直线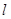 与圆
与圆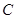 交于
交于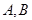 两点,试求弦
两点,试求弦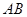 的长.
的长.
现要设计一个如图所示的金属支架(图中实线所示),设计要求是:支架总高度AH为6米,底座BCDEF是以B为顶点,以CDEF为底面的正四棱锥,C,D,E,F在以半径为1米的圆上,支杆AB⊥底面CDEF.市场上,底座单价为每米10元,支杆AB单价为每米20元.设侧棱BC与底面所成的角为θ.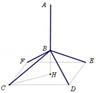
(1)写出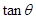 的取值范围;
的取值范围;
(2)当θ取何值时,支架总费用y(元)最少?
(本小题满分12分)已知曲线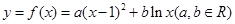 在点
在点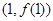 处的切线的斜率为1.
处的切线的斜率为1.
(1)若函数f(x)的图象在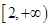 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;
(2)当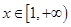 时,不等式
时,不等式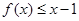 恒成立,求a的取值范围.
恒成立,求a的取值范围.
已知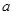 为实数,函数
为实数,函数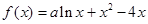 .
.
(1)是否存在实数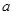 ,使得
,使得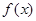 在
在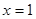 处取得极值?证明你的结论;
处取得极值?证明你的结论;
(2)设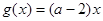 ,若
,若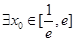 ,使得
,使得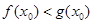 成立,求实数
成立,求实数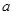 的取值范围.
的取值范围.
已知直线的极坐标方程为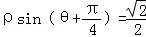 ,圆M的参数方程为
,圆M的参数方程为 (其中θ为参数).
(其中θ为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆M上的点到直线的距离的最小值.