(本小题满分12分)为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分按每度0.5元计算.
(1)设月用电x度时,应交电费y元.写出y关于x的函数关系式;
(2)小明家第一季度交纳电费情况如下:
则小明家第一季度共用电多少度?
已知函数 ,
, .且
.且 为奇函数,
为奇函数,
(1)求 的值;
的值;
(1)若函数f(x)在区间(-1,1)上为增函数,且满足f(x-1)+f(x)<0,求x 的取值集合。
(本小题满分12分)设数列 的前
的前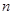 项和
项和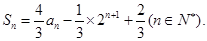
(1)求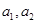 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)设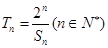 ,证明:
,证明:
(本小题满分12分)已知向量 .
.
(1)求 与
与 的夹角的余弦值;
的夹角的余弦值;
(2)若向量 与
与 平行,求
平行,求 的值.
的值.
(本小题满分14分)已知椭圆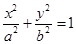 (
( )经过点
)经过点 ,且椭圆的左、右焦点分别为
,且椭圆的左、右焦点分别为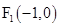 、
、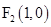 ,过椭圆的右焦点
,过椭圆的右焦点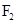 作两条互相垂直的直线,分别交椭圆于点
作两条互相垂直的直线,分别交椭圆于点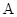 、
、 及
及 、
、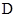 .
.
(1)求椭圆的方程;
(2)求 的值;
的值;
(3)求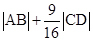 的最小值.
的最小值.
某机床厂2011年年初用98万元购进一台数控机床,并立即投入生产使用.计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元;该机床使用后,每年的总收入为50万元.
设使用 年后数控机床的盈利额为
年后数控机床的盈利额为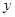 万元.
万元.
(Ⅰ)写出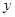 与
与 之间的函数关系式;
之间的函数关系式;
(Ⅱ)使用若干年后,对机床的处理方案有两种:
方案一:当年平均盈利额达到最大值时,以 万元价格处理该机床;
万元价格处理该机床;
方案二:当盈利额达到最大值时,以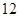 万元价格处理该机床;
万元价格处理该机床;
请你研究一下哪种方案处理较为合理?并说明理由.
已知数列{an}各项均为正数,其前n项和为Sn,且满足4Sn=(an+1)2.
(1)求{an}的通项公式;
(2)设bn= ,求数列{bn}的前n项和为Tn
,求数列{bn}的前n项和为Tn
(本小题满分14分)在平面直角坐标系 中,已知
中,已知 的顶点坐标为
的顶点坐标为 .
.
(1)求直线 的方程;
的方程;
(2)求边 上高
上高 所在的直线方程.
所在的直线方程.
(本小题满分13分)如图,在直角坐标系 中,角
中,角 的顶点是原点,始边与
的顶点是原点,始边与 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点 ,且
,且 ,将角
,将角 的终边按逆时针方向旋转
的终边按逆时针方向旋转 ,交单位圆于点
,交单位圆于点 ,记
,记 .
.
(1)若 ,求
,求 ;
;
(2)分别过 作
作 轴的垂线,垂足依次为
轴的垂线,垂足依次为 ,记
,记 的面积为
的面积为 ,
, 的面积为
的面积为 ,若
,若 ,求角
,求角 的值.
的值.
(本小题满分10分) 中,
中, 分别为角
分别为角 所对的边.
所对的边.
(Ⅰ)若 成等差数列,求
成等差数列,求 的值;
的值;
(Ⅱ)若 成等比数列,求角
成等比数列,求角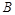 的取值范围.
的取值范围.