已知函数 的图象经过点
的图象经过点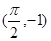 .
.
(1)求函数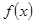 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.
(2)若 ,且
,且 ,求
,求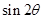 的值.
的值.
(本小题满分10分)
(Ⅰ)证明: .
.
(Ⅱ)已知圆的方程是 ,则经过圆上一点
,则经过圆上一点 的切线方程为
的切线方程为 ,类比上述性质,试写出椭圆
,类比上述性质,试写出椭圆 类似的性质.
类似的性质.
已知
(1)若 ,求实数m的取值范围;
,求实数m的取值范围;
(2)是否存在实数m,使得“ ”是“
”是“ ”的充要条件,若存在,求出m的取值范围;若不存在,请说明理由.
”的充要条件,若存在,求出m的取值范围;若不存在,请说明理由.
(本小题满分13分)已知椭圆 的左焦点为
的左焦点为 .
.
(1)设椭圆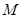 与函数
与函数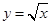 的图像交于点
的图像交于点 ,若函数
,若函数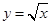 在点
在点 处的切线过椭圆的左焦点
处的切线过椭圆的左焦点 ,求椭圆的离心率;
,求椭圆的离心率;
(2)设过点 且斜率不为零的直线
且斜率不为零的直线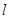 交椭圆于
交椭圆于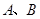 两点,连结
两点,连结 (
( 为坐标原点)并延长,交椭圆于点
为坐标原点)并延长,交椭圆于点 ,若椭圆的长半轴长
,若椭圆的长半轴长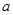 是大于1的给定常数,求
是大于1的给定常数,求 的面积的最大值
的面积的最大值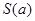 .
.
(本小题满分13分)已知函数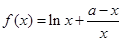 ,其中
,其中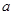 为常数,且
为常数,且 .
.
(Ⅰ)若曲线 在点(1,
在点(1,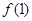 )处的切线与直线
)处的切线与直线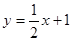 垂直,求
垂直,求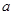 的值;
的值;
(Ⅱ)若函数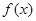 在区间[1,2]上的最小值的表达式.
在区间[1,2]上的最小值的表达式.
(本小题满分12分)在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=1,AB=4,BC=2 ,∠CBA=30°.
,∠CBA=30°.
(1)求证:AC⊥PB;
(2)当PD=2时,求此四棱锥的体积.
已知两直线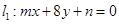 和
和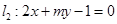 ,试确定
,试确定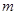 ,
,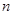 的值,使(1)
的值,使(1) ;(2)
;(2) ,且
,且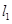 在
在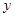 轴上的截距为-1.
轴上的截距为-1.
(本小题满分12分) 设函数
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)令 <
< ≤
≤ ,其图像上任意一点P
,其图像上任意一点P 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,方程
时,方程 在区间
在区间 内有唯一实数解,求实数
内有唯一实数解,求实数 的取值范围。
的取值范围。